LAST MODIFIED Friday, December 19, 2003 12.20 AM PT
THIS DOCUMENT IS NOW FROZEN. TO TRACK LATER CHANGES, SEE INSTEAD
http://www.ihmc.us/users/phayes/SCL_december_3.HTML
SCL is a first-order logical language intended for information exchange and transmission. SCL allows for a variety of different syntactic forms, called skins, all expressible within a common XML-based syntax and all sharing a single semantics.
SCL has some novel features, chief among them being the ability to express the signature of an SCL ontology in the ontology itself, a syntax which permits 'higher-order' constructions such as quantification over classes or relations, and a semantics which allows theories to describe intensional entities such as classes or properties. It also uses a few conventions in widespread use, such as numerals to denote integers and quotation to denote character strings, and has provision for the use of datatypes, and for naming, importing and transmitting content on the WWWeb.
<history: KIF, CL, unification, reducing complexity; needs of the SW.>
It is clear that the 'same' logical expression can be rendered in a variety of different syntactic, or even graphical, forms: connectives can be written as infix, postfix or prefix, groupings indicated by brackets, groups of dots or graphically by enclosing circles, etc.. The differences in appearance between surface forms can be quite extreme. A simple logical expression written in introductory text-book form:
(∀x)(Boy(x) → (∃y)(Girl(y) & Kissed(x,y)))
appears in conceptual graph interchange form (CGIF) as:
[@every*x] [If: (Boy ?x) [Then: [*y] (Girl ?y) (Kissed ?x ?y) ]]
and in a KIF-like syntax as:
(forall (?x ?y)
(implies (Boy ?x))
(exists (?y)
(and (Girl ?y)
(Kissed ?x ?y))))
Extremely 'compact' notations have been used, such as the postfix convention which requires no parentheses:
KissedxyGirly&EyBoyxIAx
while at the other extreme, a hypothetical XML notational style might look like
<formula>
<forall>
<var>x</var>
<formula>
<implies>
<formula>
<atom>
<con>Boy</con>
<var>x</var>
</atom>
</formula>
<formula>
<exists>
<var>y</var>
<formula>
<and>
<formula>
<atom>
<con>Girl</con>
<var>x</var>
</atom>
</formula>
<formula>
<atom>
<con>Kissed</con>
<var>x</var>
<var>y</var>
</atom>
</formula>
</and>
</formula>
</exists>
</formula>
</implies>
</forall>
</formula>
To provide for information exchange between such a plethora of syntactic alternatives,
SCL follows the lead of the KIF initiative by providing a single 'standard'
logical language, called the SCL core, and a general technique for
translating other notations, called SCL dialects, into the core syntax.
In fact, only a subset of the
SCL can be expressed a variety of dialects, and this document defines several which provide SCL variants similar to existing logical notations in widespread use, and an XML-based syntax, XCL, for general purposes of information exchange. XCL allows assertions to declare their dialect, and so can be used as a general-purpose interchange notation and mark-up language for any conforming SCL syntax. Finally, a general technique for defining SCL skins in terms of an SCL abstract syntax is described.
In addition to providing for many divergent surface syntactic forms, SCL is designed to allow expressions to be used without making explicit lexical assumptions. Conventionally, a first-order language is defined relative to a particular signature, which is a lexicon sorted into disjoint sublexica of individual names, relation names and perhaps function names, the latter each associated with a particular arity, i.e. a number of arguments with which it must be provided. This provides a simple context-free method of checking that all terms and atomic sentences will be well-formed, and ensures that any expression obtained by substitution of well-formed terms for variables will be assigned a meaningful interpretation.
The notion of signature is appropriate for textbook uses of logic. Applied to an interchange situation, however, where sentences are distributed and transmitted over a network (in particular, on the WWWeb) and may be utilized in ways that are remote from their source, this would require that a single global convention for signatures be adopted, which is impractical. SCL therefore is designed to have no built-in assumptions about signatures: it allows information to be combined even when it is written using divergent assumptions about the appropriate signature. This has a number of consequences.
First, SCL must be able to accomodate expressions in which a term is used both as an individual name and as a relation name, or cases where a relation name is used with different numbers of arguments, or as both a relation and a function name. To this end, SCL is defined with a very accomodating syntax which places minimal restrictions on the lexical roles of names or indeed of terms more generally, and allows relationships between alternatives to be expressed in the language itself.
Such cases arise often in practice. For example, the idea of marriage can be rendered in a formal ontology as a binary relation between persons, or a more complex relation between persons, legal or ecclesiastical authorities and times; or as as a legal state which 'obtains', or as a class or category of 'eventualities', or as a kind of event. Much the same factual information can be expressed with any of these ontological options, but resulting in highly divergent signatures in the resulting formal sentences. Rather than requiring that one of these be considered to be 'correct' and the others translated into it by some external syntactic transformation, SCL allows them all to co-exist, often allowing the connections between the various ontological frameworks to be expressed in the logic itself. For example, consider the following sentences (all written in the SCL core syntax):
married(Jack Jill)
married{husband=Jack wife=Jill}
exists (x) (married(x) & husband(Jack x) & wife(Jill x))
when(married(Jack Jill))=hour(3 pm(thursday(week(12 year(1997)))))
wife(married(32456))=Jill
ConjugalStatus(married Jack)
ConjugalStatus(Jack)(Jill)
These all express similar propositions about a Jack and Jill's being married,
but in widely different ways. The logical name married appears
here as a binary relation between people, a unary property of a state of affairs,
a three-place relation between two persons and a time, a function from numbers
to individuals, as an individual 'status', and finally, although not named explicitly,
as the value of a function from persons to predicates on persons.In SCL all
these forms can be used at the same time: the conjunction of the above set of
sentences is syntactically correct SCL, which does not impose any restriction
on the occurrence of terms in other atoms or terms: any term may occur
in any position in any atomic sentence or term. This allows quantification over
relations and functions, for example, or the use of relation-valued functions,
or relations applied to other relations. The resulting syntax is similar to
a higher-order syntax; but unlike traditional omega-order logic, SCL syntax
is completely type-free. It requires no allocation of higher types
to functionals such as ConjugalStatus, and imposes no type discipline.
For example, self-application is syntactically legal in SCL, as in:
is-Relation(is-Relation)
Readers familiar with conventional first-order syntax will recognize that this syntactic freedom is unusual, and may suspect that SCL is a higher-order logic in disguise. However, as has been previously noted on several occasions [ref HILOG][refHenkin?], a superficially 'higher-order' syntax can be given a completely first-order semantics, and SCL indeed has a purely first-order semantics, and satisfies all the usual semantic criteria for a first-order language, such as compactness and the Skolem-Lowenheim property.
What makes a language semantically first-order is the way that its names and quantifiers are interpreted. A first-order interpretation has a single homogenous universe of individuals over which all quantifers range, and any expression that can be substituted for a quantified variable must denote something in this universe. The only logical requirement on the universe is that is a non-empty set. Relations hold between finite sequences of individuals, and all that can be said about an individual is the relations it takes part in: there is no other structure. Individuals are 'logically atomic' in a first-order language: they have no logically relevant structure other than the relationships in which they participate. Expressed mathematically, a first-order intepretation is a purely relational structure. It is exactly this essential simplicity which gives first-order logic much of its power: it achieves great generality by refusing to countenance any restrictions on what kinds of 'thing' it talks about: it requires only that they stand in relationships to one another.
Contrast this with for example higher-order type theory, which requires an interpretation to be sorted into an infinite heirarchy of types, satisfying very strong conditions. In HOL, a quantification over a higher type is required to be understood as ranging over all possible entities of that type; often an infinite set.
In FO semantics, a relation name is interpreted as denoting a set of sequences of individuals, being the sequences between which the relation holds: call this a relation set, or a relational extension. In the SCL syntax, the same name can be used to refer to an individual. To retain the essentially first-order nature of the interpretation in cases like this, SCL assumes that a relation name used as an individual name must refer to an individual which, if it is ever called upon the play the role of a relation, is true of exactly the same sequences. The relational individual is 'associated' with same relation set as its name. This ensures that the name retains a single meaning in all contexts of use. In stating the formal semantics we will call this association mapping rel, so that if <name> is intepreted both as a relation, using the mapping R, and as an individual, using I, then R(<name>)=rel(I(<name>))
Note that we do not assume that the individual denoted by the relation symbol is the relation set itself. While that interpretation might be thought set-theoretically more natural, to require an individual to be a large set containing structures containing other individuals would be a clear violation of the essentially first-order nature of SCL semantics.
This semantic strategy also allows several distinct individuals to be associated with the same relational extension, which provides an extra measure of descriptive flexibility. One can think of a relational individual as a relation in an intensional sense, and a relation set as a relation in a narrower extensional sense. SCL may be said to embody an intensional theory of relations as objects, although the SCL truth-conditions are purely extensional.
Finite sequences play a central role in SCL syntax and semantics. All atomic sentences consist of an application of one term, denoting a relation, to a finite sequence of other terms. Such argument sequences may be empty, but they must be present in the syntax, as an application of a relation term to an empty sequence does not have the same meaning as the relation term alone.
SCL also allows relations to be take any number of arguments: such a relation
is called variadic. (Married is an example of a variadic
relation.) SCL follows KIF also in providing a special syntactic form called
sequence variables to allow generic assertions to be made which apply
to arbitrary argument sequences. An SCL axiom using sequence variables can be
viewed as a first-order axiom scheme, standing in for a countably infinite set
of first-order instances.
If an argument sequence ends with a sequence variable, then the presence of the variable indicates that the sequence may be arbitrarily extended, and the sentence is required to hold for all the possible extensions.
Sequence variables are quite a powerful device: in effect, they allow a finite sentence to assert infinitely many quantifications all at the same time. Indeed, if arbitrary quantification over sequence variables is permitted, then the resulting language is a subset of the infinitary logic Lw1w, of a higher expressiveness than first-order logic, and for example is not compact [refHayMenzel]. The restrictions on sequence variables in SCL have been chosen to restrict the language to first-order while providing much of the practical utility of sequence variables for writing 'recursive' axioms to define lists and other recursively defined constructions.
Sequence variables are restricted in SCL to occur only in the last position in an argument sequence, and are not bound by quantifiers: this keeps the language first-order and makes unification tractable. Sequence variables can be replaced by a more conventional notation, at some considerable cost in elegance, by introducing argument lists to the ontology explicitly: we provide a generic header which can be used for this kind of elimination, which is commonly adopted in practical KR notations.
SCL treats functions, semantically, as a special class of relations. A relation
is functional (at n), or (n-)functional,
when it holds of a single, unique first argument for each sequence (of length
n) of the remaining arguments. The SCL convention is that the first
argument is the value of the relation applied to the remaining arguments; thus,
if R is a relation symbol denoting a 2-functional relation then
the equation a = R(b c) is is similar in meaning to the atomic
sentence R(a b c).
This differs from the convention used in Prolog [refProlog]
where the function value is written as the last argument of a relation.
The present convention was chosen to better integrate with the use of sequence
variables. Note that the arity of the function is the number of relational
arguments, so is one more than the number of functional arguments: in this case
the arity of R is 3.
The terminology is extended in an obvious way to functional above n, meaning m-functional for every m greater or equal to n. Note that functional includes the case n=0, so a functional set must contain one singleton sequence, and cannot contain the null sequence.
Assimilating functions to relations in this way is straighforward, and indeed is standard practice; but the presence of function symbols in a piece of SCL syntax greatly complicates the statement of the model theory. This is because function symbols can be used, in effect, to create new names, by substituting terms as arguments in other terms. The simple presence of a function symbol therefore provides an infinite set of names, conventionally called the Herbrand universe; and any first-order semantics must be stated in such a way that every such term has a well-defined denotation. In a conventional logical framework this is guaranteed by the signature, since every function symbol is assigned a fixed number of arguments and is required to denote a function of the appropriate arity; but for SCL a more subtle criterion is required, called fitting. An interpretation of a set of SCL sentences is required to fit those sentences, in a sense made precise below but which can be intuitively characterized as being required to provide a well-defined interpretation for every term that can be obtained by substitution of terms for variables, i.e. every possible expression which refers to an individual. The presence of variables in function terms and the use of sequence variables both impose quite strong fitting conditions, in some cases amounting to the requirement that every individual have a corresponding relational extension which is functional.
An SCL ontology, or simply an ontology, is any set or sequence of SCL sentences together with an optional header, which is itself a set or sequence of SCL sentences.
The kernel syntax uses sequences throughout, for convenience in defining iterative syntactic operations, but no particular significance attaches to the ordering of the sequence, and other SCL skins may adopt a set-based syntactic convention.
The choice of the term "ontology" is not intended to convey any particular categorization or to indicate an intended use or philosophical stance; it is intended to be a neutral terminology used to refer to a coherent piece of SCL which can be published, transmitted or asserted as a single document: the topmost level of the syntax. Other synonyms in widespread use in various communities include "knowledge base", "axiom set" , "set of sentences", "metadata", "data model" and "model", as well as such particular usages as "RDF graph" and "document".
Headers have a special semantic role and are treated in a distinct way in the semantics: they provide a general method for encoding syntactic and other 'background' information about the ontology. A special header theory is provided, of relations with a fixed interpretation, sufficient to describe many standard signatures and syntactic conventions.
The core also provides a top-level ontology definition syntax which associates a name with an ontology, and a importing syntax, which indicates that a named ontology is being included into an ontology. The intended meanings of these constructions is fairly obvious, but the formal semantic statement requires that we assume the existence of a global ontology-naming convention which transcends particular ontologies and particular interpretations, and that ontology names refer to entities in formal interpretations. This can all be stated abstractly, but is more directly conveyed by the observation that SCL uses the emerging semantic web conventions based on the W3C URI naming protocols [ref RFC2396].
Comment. KISS.
The SCL Core is the basic syntactic form of SCL relative to which the semantics is defined, and which is used to give examples throughout this document. It is not the recommended SCL syntax for information exchange. The choice of syntax for the core is somewhat arbitrary, but was based on KIF for historical legacy reasons and because this form, although slightly unconventional in appearance to an eye accustomed to textbook logical forms, has several advantages for machine processing. The SCL core syntax is not exactly that of KIF 3.0 [refKIF], and it defines a considerably smaller language.
Apart from being a smaller language, SCL Core syntax differs
from KIF in the following respects.
(1) Variables are not required to be marked syntactically, and free variables
are impossible.
(2) The double-quote symbol " is prohibited in SCL Core. This permits quoted
SCL Core syntax to be included inside XHTML markup without being rendered by
a Web browser. Otherwise, SCL Core syntax permits the use of the full Unicode
character set.
(3) .... finish this list later
do lexicon first
Any SCL Core, or core, expression is encoded as a sequence of Unicode characters ( UCS-2, from the Unicode 'base multilingual plane' according to ISO/IEC 10646-1:1999). The standard encoding is UTF-8 (ISO 10646-1:2000 Annex D ) . Only characters in the US-ASCII subset are reserved for special use in the core itself, so that the language can be encoded as an ASCII text string if required. UCS-2 characters outside that range are represented in ASCII text by a character coding sequence of the form \unnnn or \unnnnnn where n is a hexadecimal digit character. When transforming an ASCII text string to UTF-8, such a sequence should be replaced by the corresponding UTF-8 byte encoding. This document uses the ASCII encoding.
The syntax of the core is designed to be easy to process mechanically. The syntax is defined in terms of disjoint blocks of characters called lexical items or lexemes . A character stream can be converted into a stream of lexemes by a simple process of lexicalisation which checks for a small number of interlexical characters, which indicate the end of a lexical item (and sometimes the start of the next one.) The interlexical characters are: single quote ' (U+0060), open and closing parenthesis ( U+0028 and U+0029) and any whitespace character: in ASCII, these are space (U+0020), tab (U+0009) line (U+000A) page (U+000C ) and return (U+000D) The backslash character \ (reverse solidus U+005C) also plays a role in lexicalization, by cancelling the interlexicality of the immediately following character. Certain characters are reserved for special use as the first character in a lexical item, and the characters less-than < (U+003C), greater-than > (U+003C) and double-quote " (U+0022) are forbidden, and should be replaced by a suitable encoding, which may be the Unicode character coding sequence described above, or another character encoding mandated by the conventions used in any surrounding or enclosing document.
The backslash \ (reverse solidus U+005C) character is reserved for special use. Backslash \ plays a special role in enabling "out of code" characters to be included in core text. Followed by the lowercase letter u (U+0075) and a four- or six-digit hexadecimal code, it is used to transcribe non-ASCII UTF-8 characters, as explained above. Any string of this form plays the same syntactic role in an ASCII string rendering as a single ordinary character. Backslash is also used as a cancelling prefix. The special roles of any of the interlexical or marking characters, and of the backslash character itself, can be cancelled by preceding the character with a backslash. This enables marking and interlexical characters to be included in lexical items without writing their Unicode equivalents, and permits hexadecimal Unicode codes to be transmitted as ASCII character strings in contexts which would otherwise require Unicode conversion.
The following syntax is written using EBNF: | indicates alternatives, * indicates any sequence of expressions, + indicates any nonempty sequence and parentheses are used as grouping characters. The EBNF also applies to UTF-8 encodings, with the change noted to the category nonascii.
1. Character classification
S ::= (space|tab|line|page|return)+
lexbreak ::= S | '(' | ')'
alpha ::= 'A'|...|'Z'|'a'|...|'z'
digit ::= '0'|...|'9'
marker ::= '@' | '''
other ::= any other ASCII non-control character
2. Lexical analysis
hexa ::= digit|'A'|...|'F'|'a'|...|'f'
nonascii ::= '\u' hexa hexa hexa hexa| '\u' hexa hexa hexa hexa hexa hexa
Note. For UTF-8 strings, nonascii is the set of all non-control characters of UTF-8 outside the ASCII range, ie all non-control characters in the range U+007F-FFFFFD. The use of the \uXXXX sequence in UTF-8 character strings, while not illegal, is deprecated.
wordchar ::= alpha | digit | marker | nonascii
stringchar ::= wordchar | lexbreak | '\''
quotedstring ::= ''' stringchar* '''
Note. Quoted strings are the only lexical items that can contain whitespace. A quoted string can contain any character, but a single quotemark ' can occur inside a quoted string only when immediately preceded by a backslash, which also acts as a self-cancelling prefix when it precedes itself. For example, the quotedstring 'a\b\\\'cd\'' indicates the string: a\b\'cd'.
lexitem ::= wordchar* | '(' | ')' | string
Note. lexitem is an "umbrella" category which includes all lexical items. The job of a lexical analyser is to divide the input character stream into a stream of non-overlapping lexical items, possibly separated by lexbreak characters. The rest of the SCL core syntax can be characterized in terms of a sequence of lexical items.
3. Lexical syntax
specialname ::= 'and' | 'or' | 'iff' | 'implies' | 'not' | 'scl:imports' |
'scl:arity' | 'scl:Ind' | 'scl:Rel' | 'scl:header' | numeral
word ::= ( ( alpha | other | insert ) wordchar* ) - specialname
seqvar ::= '@' wordchar+
numeral ::= digit+
Note. A word is any lexical item that does not start with a marking character (though it may include them.) Specialname is a category of names which are reserved for use by SCL. Other SCL dialects may extend this category to include other name forms reserved for special use, and headers may declare classes of special names. Numerals and special names should not be used as names; if they are so used, their interpretation as numerals or special names overrides any meaning assigned to them by other uses.
4. Core expression syntax
Note. All core expressions consist of a pair of parentheses enclosing the logical subexpressions of the expression in question, usually with a word immediately following the opening parenthesis which indicates the logical category of the expression. The role of whitespace and parentheses in the syntax can be summarized by the observation that whitespace is always optional except to separate names in a term sequence, and that syntactic divisions between expressions are mostly indicated by the occurrence of parentheses.
termseq ::= (term S?)* seqvar?
term ::= name | specialname | '('term S termseq S? ')' | '('quotedstring S term
S? ')'
equation ::= '(=' S? <term> S <term> S? ')'
atom ::= '(' S? term S termseq S? ')' | '(' S? term S rolepair* S? ')' | equation
rolepair::= '(' S? name S '=' S term S? ')'
boolsent ::= '(' (( 'and' | 'or' ) S)? (<sent> S?)* ')' | '(' ( 'implies'|'iff'
) S? sent S? sent S? ')' | '(not' S? sent S?')'
quantsent ::= '(' ( 'forall' | 'exists' )? '(' ( name | '('name S name ')' )*
')' S? sent S? ')'
sent ::= atom | boolsent | quantsent | '('quotedstring S? sent ')'
topsentence ::= '(scl:import' S name S? ')' | sent | '(' quotedstring ')'
module ::= '(' ( '(scl:header' ( topsent S?)* ')' )? (topsent S?)* ')'
ontologydefinition ::= '(scl:ontology' S? name S? '=' S? ontology S? ')'
The kernel is a minimal subset of the core expression syntax with a restricted sentence syntax which is sufficient to express the content of any core expression. The only connective used is 'not'; conjunction is indicated by listing the conjuncts within parentheses, and the universal quantifier is indicated by a bound-variable list enclosed in parentheses.
termseq ::= (term S?)* seqvar?
term ::= name | specialname | '('term S termseq S? ')' | '('quotedstring S term
S? ')'
equation ::= '(=' S? <term> S <term> S? ')'
atom ::= '(' S? term S termseq S? ')' | equation
sent ::= atom | '(' (sent S?)* ')' | '(not' S? sent S?')' | '(' S? '(' name
')' S? sent S? ')' | '('quotedstring S? sent ')'
topsentence ::= '(scl:import' S name S? ')' | sent | '(' quotedstring ')'
module ::= '(' ( '(scl:header' ( topsent S?)* ')' )? (topsent S?)* ')'
ontologydefinition ::= '(scl:ontology' S? name S? '=' S? ontology S? ')'
-------
Give translation table from core into kernel, without making a fuss about it. Remark that this is simple example of a dialect, more details later.
Apart from the top-level syntax for defining headers and ontologies, the only unconventional aspects of SCL are the syntax for atomic sentences and terms, which reflect the type-free catholicity imposed by the need to allow multiple lexical perspectives within a single ontology. This section discusses these features in more detail.
A sequence variable stands for an 'arbitrary' sequence of arguments. Since
sequence variables are implicitly universally quantified, any top-level expression
in which a sequence variable occurs has the same semantic import as the countably
infinite conjunction of all the expressions obtained by replacing the sequence
variable by a finite sequence of variables, all universally quantified at the
top level. For example, the top-level sentence R(@x) occurring
in an ontology has the same meaning as the infinite conjunction
R() & (x)R(x) & (x)(y)R(x y) & (x)(y)(z)R(x y z) ...
Note . This includes the empty-sequence case. To avoid this,
use a variable followed by a sequence variable: R(x @y).
Sequence variables can be used to write 'recursive' axiom schemes. Rather than attempt a fully general description of this technique, we will illustrate it with a canonical example. Consider the following sentences:
nil = list()
(x)(y)(z)( x = list(@y) iff cons(z x) = list(z @y) )
which have the same meaning as the infinite set of sentences:
(nil = list()
(x)(y)(z) x = list() iff cons(z x) = list(z) )
(x)(y)(z)(x1) x = list(x1) iff cons(z x) = list(z x1) )
(x)(y)(z)(x1)(x2) x = list(x1 x2) iff cons(z x) = list(z x1 x2) )
(x)(y)(z)(x1)(x2)(x3) x = list(x1 x2 x3) iff cons(z x) = list(z x1 x2 x3) )
...
(x)(y)(z)(x1)(x2)...(xn) x = list(x1 ... xn) iff cons(z x) = list(z x1 ... xn)
)
... )
which clearly entails for any finite sequence t1... tn of terms,
that
cons(t1 cons(t2 cons(...cons(tn nil)...)) = list(t1 ... tn)
and thus provides the familiar technique of writing a sequence of items as a cons-nil list, first used in LISP and more recently as the RDF 'collection' vocabulary [refRDF]. The tail-recursion represented by the axiom is re-expressed here as induction on the length of a proof.
Technical note. SCL seqvars do not actually provide a true recursive definition, as the 'schema' can be used only as a source of assertions and cannot itself be derived by using an inductive argument. The more powerful language obtained by allowing sequence variables to be bound by sequence quantifiers does provide true recursive powers, and is therefore in a higher expressive class than any first-order language. It is, for example, not compact.
This general technique of imitating tail-recursive definitions by writing them as implications using sequence variables was pioneered by KIF [refKIF] and is one of the primary uses for sequence variables in SCL. What this construction shows, however, is that the use of sequence variables can be replaced, when required, by the use of explicit cons-nil lists as arguments, represented in SCL by nested terms. The general rule can itself be stated in SCL by using seqvars:
(x) x(@y) iff x(list(@y))
This thus provides a general technique for replacing the use of sequence variables by explicit quantification over argument lists. The costs of this translation are a considerable reduction in syntactic clarity and readability, and the need to allow lists as entities in the universe of discourse; the advantages are the possibility of rendering arbitrary argument seqences using only a small number of primitives with a fixed, low arity. SCL can use either convention or both together, and can describe the relationship between them.
Atomic sentences of the form
Married{wife=Jill husband=Jack}
are considered to take a set of arguments in the form of role-value pairs. (The kernel translation assumes that this set has been ordered in some arbitrary way.) In this role-set syntax, the connection between the relation and its arguments is indicated by the role labels rather than by position in an argument sequence, which avoids the necessity of remembering the argument order when writing sentences, and provides some insurance against errors arising from sentences using different argument-order conventions.
In SCL, the roles are considered to be binary relations between an entity to which the main predicate applies and the argument, so for example the above atom is equivalent to the existential conjunction:
exists (x) Married(x) & Jack=husband(x) & Jill=wife(x)
where x indicates an entity which has been variously called an
eventuality, fact, situation, event, state or trope,
and might be rendered in English as "Jack and Jill's being married"
or "the marriage of Jack and Jill". For SCL purposes however it is
possible to think of x more prosaically as being an argument sequence,
and the role-names as selectors on the elements of this sequence.
This syntax allows arguments to be provided in a piecemeal
fashion, and allows arguments to be omitted: such arguments are implicitly existentially
quantified. In fact, any such atom entails a similar atom with some role-pairs
omitted. Notice the difference in meaning between R() and R{
}. The former asserts positively that R is true of the empty
sequence, while the latter merely asserts that R is true of something,
to which other things may be related by unknown roles; for example, Married{
} asserts simply that a marriage exists, and might be rendered as "marriedness
is manifested".
This role-set convention does not of itself specify any relationship between the same fact expressed as an argument set and using an argument sequence: but since SCL allows variadic relations, it is possible to use the same relation in both ways, and they can be related axiomatically by for example writing
( Married(x y) & Married(z) ) implies ( x=wife(z) & y=husband(z)
)
which indicates the convention by which a wife must be the first argument of a marriage. Again, SCL provides for both kinds of syntax, separately or together, and can describe the relationship between them using SCL axioms.
Any term which occurs as the first term in any atomic sentence or term is said to occur in relation position; any term which occurs as the first term in any other term of the form t(t1 ... tn) is said to occur in a function position on n; if it is the first term in another term of the form t(t1 ... tn @x) with a sequence variable then it said to occur in function position above n, or equivalently to occur in function position on m for all m>=n; and finally, any term occurring as an argument of any other term or atom is said to occur in object position. These generalize the usual notions of signature category for relation, function and individual names; but note that the function positions are consiered to be subcategories of relation position.
If O is an ontology then a term occurs in O in some position just when it occurs in that position in any atom or term occurring as a subexpression anywhere in O. A single term may occur in more than one position.
GOFOL; rigid; relational
<summary of holds/app translation>
Throughout this section we will consider only the SCL kernel, which provides a minimal syntax on which to attach the semantics.The semantics of other SCL skins (including the SCL core) are defined by their translation into the SCL kernel. Recall that the kernel syntax treates variables as a category of names.
The semantics of SCL is defined in terms of a satisfaction relation between ontologies and structures called interpretations, in the conventional way. For SCL however we must first define a notion of an interpretation fitting an ontology. As discussed earlier, this generalizes the usual idea of an interpretation being defined on a fixed signature: in effect, an intepretation fits an ontology when it is an interpretation in the conventional sense of some possible signature under which the ontology could be syntactically legal.
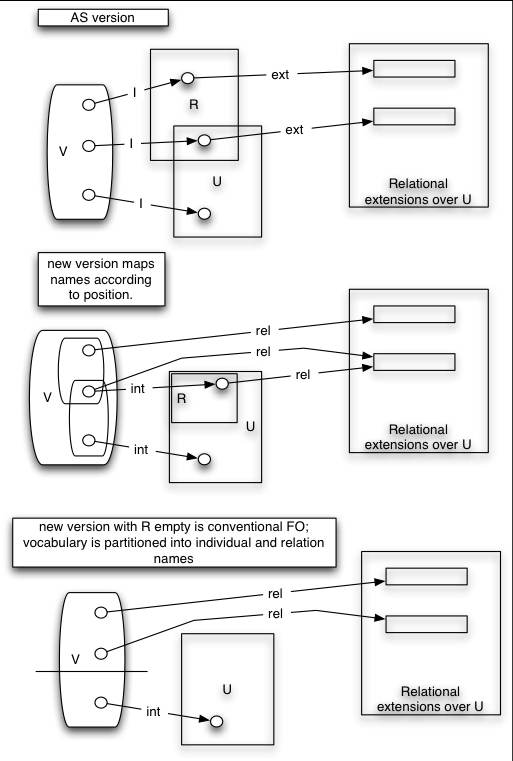
This is essentailly the same MT as in Chris' document, but with the ext mapping treated differently. Heres the summary picture:

The idea is to give an intuitive story for what 'ext' (now rel) means: its the extension of the ordianry semantic mapping for relation *symbols* into the universe so as to provide for individuals playing the role of relations. This is quite a pretty picture: one can view the 'fitting' conditions as a kind of induction which forces rel into the universe in appropriate ways to ensure that enough relations exist - but its chief advantage is that it preserves the GOFOL case strictly, in that the MT is then exactly conventional.
The downside is that the MT conditions for atoms and terms have to be stated twice, once using rel(v) for relation names and onceusing rel(I(t)) for other terms; but this is a small price in elegance, I think. Also having a lexical category of 'pure' relation symbols even in the full wild-west syntax is quite useful eg in simplifying the holds/app translation. And it clarifies why some relations need not be in the universe.
This combines Chris' idea for handling the Horrocks sentences by allowing R to escape U with the older idea of R being the subset of U which is the relational individuals. We adopt the latter, but handle the former by letting relation names which are not used as individuals to denote extensions directly. This has no consequences for intensional relational theories since they always have those relations in the universe in any case.
A vocabulary is a set of names. An interpretation on O is defined by a set and two mappings:
A nonempty set UI called the universe;
A mapping intI from names in object position in O to UI;
A mapping relI from names in relation position in O to the set RelI of sets of finite sequences of elements of UI
such that if v is in function position on n in O then relI (v) is functional on n.
This is a conventional first-order interpretation structure; although note that the when sequence variables are present, the condition on functionality may apply to functions of infinitely many arities.
The lexical freedom of SCL requires us to extend this in order to guarantee that all terms which may occur in a functional or relational role are given an interpretation. We do this by extending the relational interpretation mapping relI from the lexicon into the universe, allowing individuals to play a relational role. We will define RI to be the subset of UI on which relI is defined; elements of RI are called relational individuals.
Every interpretation is required to satisfy the basic fitting condition: for any name v occurring in both object and relation position, then intI (v) is in RI and
relI(intI (v))= relI(v)
As discussed earlier, this simply ensures that the relational individual denoted by a relation name will play the same relational role as the name itself.
This is the 'convergent arrow' case in the middle diagram.
However, SCL also allows variables to occur in arbitrary positions, and so we must ensure that relI is extended appropriately to entities which may be denoted by terms containing variables.
Define a name map on a set S of names to be any mapping from S to UI, and a sequence variable map similarly from sequence variables to finite sequences of elements of UI, and define IA to be the mapping which is like A on variables and seqvars, but otherwise is like I: formally,
intIA(v) = A(v) when v is in S, otherwise intIA(v)= intI(v); and relIA(v) = A(v) when v is in S, otherwise relIA(v)= relI(v)
This notation associates to the left, so that IAB = (IA)B, meaning that if x is in the domain of B then intIAB(x)=B(x).
Say that I fits O when for every sequence map A on the sequence variables in O, and name map B on the variables in O, IAB satisfies the interpretation conditions applied to the relational individuals. In order to state this precisely, we need to refer to the semantics for terms, defined below. Strictly, the definition of 'fit' is mutually recursive with the definition of the model theory.
For any term t in relation position, relIAB(IAB(t)) is defined; and if t is in n-functional position, then relIAB(IAB(t)) is functional on n.
Because this applies for all variable maps, the presence of a variable in a relation position requires that the entire universe of any fitting interpretation consist of relational individuals, so that RI = UI. This is in fact a trivial requirement, since one can simply define relI(x)={ } for all x to which no stronger constraint applies. The presence of a variable in a function position has less trivial consequences, since it requires all individuals to be associated with functional extensions.
The fitting requirement can be read off the atom and term syntax. For example,
if there is an atomic sentence of the form a(x)(z) where x
is a variable, then relI must map I(a) into
a 1-functional extension, every value of which must be mapped by relI
into a relation. (Note that this second requirement applies only to the range
of I(a).) The presence of a sequence variable in the body of a
term with a variable in the function position, such as R(x(@z)),
imposes a strong requirement on relI : it must map everything
in U to an extension which is functional on every arity.
It is clear that these conditions can always be satisfied, for example by choosing a universal functional value c in O and defining relI (x) to be the set of all tuples with c in first position for all x in O. This makes everything in the universe into a relational individual with a fully functional extension for every arity. Of course, this interpretation may not satisfy the ontology, but its possibility does ensure that the truth-recursions which define satisfaction are well-defined.
The interpretation of an expression E, written I(E) , is then defined by the following conditions:
| SCL interpretation I of an expression E | ||
| if E is a | of the form | then I(E) = |
| plainname | n | intI(n) |
| specialName | ||
numeral |
the decimal value of numeral | |
'string' |
string with occurrences of \ preceding \ or ' deleted | |
scl:Integer |
relI(E) = {<n>: n an non-negative integer } | |
scl:String |
relI(E) = {<u>: u a Unicode character string } | |
scl:Ind |
relI(E) = {<x1,...,xn> : x1,...,xn all in UI } | |
scl:Rel |
relI(E) = {<x1, ..., xn>: x1,..., xn all in RI } | |
scl:Fun |
relI(E) = {<m, x1, ..., xn>: x1,...,xn all in RI and relI(x1),...,relI(xn) all functional on m | |
scl:Arity |
relI(E) = {<m, x1, ..., xn >: x1,...,xn all in RI and relI(x1),...,relI(xn) all contain an s with length(s)=m | |
| term sequence | (t1 ... tn) |
<I(t1),..., I(tn)> |
(t1 ... tn @v) |
<I(t1),..., I(tn) ; I(@v)> |
|
| term | f seq |
x, where relI(I(f)) or relI(f)
contains <x ; I(seq)> |
| atom | r seq |
true if relI(I(r)) or relI(r)
contains I(seq), otherwise false |
t1 = t2 |
true if I(t1) = I(t2), otherwise false | |
| booleanSentence | (not s) |
true if I(s) = false, otherwise false |
(s1 ... sn) |
true if I(s1) = ... = I(sn) = true, otherwise false | |
| quantifiedSentence | (var) body |
if for every B on {var}, IB(body) = true, then
true; otherwise, false. |
sent |
if for every A on the seqVars in sent, IA(sent) = true, then true;
|
|
This carries the truth-recursion up to top-level sentences. In order to describe the interpretation of headers we need a new notion. Say that an interpretation I is a shrinking of J, and that J is an expansion of I, when I can be obtained from J by deleting some things from the universe of I and some names from the vocabulary. Formally, when the vocabulary of I is a subset of that of J, intI(v) =intJ(v) and relJ(v)=relJ(v) for all v in the vocabulary of I; UI is a subset of UJ, RI is a subset of RJ, and for all x in RI, relJ(x) = relI(x). Intuitively, the expansion J may include new individuals and some entirely new relations, but it cannot change the extensions of relations named in I. Then we will say that
| if E is an | of the form | then I(E) = |
| ontology | (head :: body) |
if I(body)=true and for some expansion J of
I, J(head)=true, then true; otherwise
false |
The reason for requiring that an expansion of I satisfies the head of an ontology, rather than I itself, is because in general the header may use relations which are not in the intended signature of the body, and may need to quantify over entities, such as relations of the ontology, that are not in the intended universe of discourse. This allows the header to use syntax which might be forbidden by the restrictions of some SCL subcase, such as GOFOL; in fact, the primary usefulness of headers is to provide a way to describe such restrictions in SCL itself.
The two remaining constructions allow ontologies to be given global names and to be imported into other ontologies. The idea of naming an ontology makes sense only if we can assume some 'global' naming convention which has a larger scope than a single ontology, and which interpretations are required to respect. In XCL we will use URI references as global names. in accordance with the emerging WWWeb conventions, which are elaborately described elsewhere. For semantic purposes, we simply assume that there is a fixed function ont from ontology names to ontology values. The exact nature of ontology values is not specified, other than that they are entities which can be parsed into SCL kernel syntax and to which an interpretation mapping can be applied. (One can think of an ontology value as a quoted string containing a character representation of an ontology written using the kernel syntax.)
| if E is an | of the form | then I(E) = |
| topsentence | (scl:import name) |
false if I(ont(name)) = false, otherwise true |
| ontology definition | (scl:ontology name = ontology) |
if for any interpretation J, J(ont(name))
= true iff J(ontology) = true, then true; otherwise
false. |
An assertion of an ontology definition is required to have miraculous semantic powers: if it is ever true in any interpretation, then the name is attached to the defined ontology in all interpretations. Thus, if by convention we say that publishing any SCL ontology definitions amounts to asserting it, then a publication of an ontology definition requires any interpretation of any SCL ontology containing an importation of that name to treat it as having the same effect as copying out the sentences of the defined ontology in place of the importation. To actually achieve such miraculous powers requires a global naming convention: XCL uses universal resource identifiers [refRFC2396] for this purpose.
More to come.