This document was written by Pat Hayes. It represents the combined efforts of the SCL working group, a self-selected group comprising Murray Altheim, Bill Anderson, Pat Hayes, Chris Menzel, John F. Sowa, and Tanel Tammet. Contributions were also made by Michael Gruninger, Geoff Sutcliffe, Kenneth Murray, Jay Halcomb, Robert E. Kent, David Fraenkel and Mark Stickel. The work was an outgrowth of earlier work by the KIF/CL working group comprising, in addition to the above, Adam Pease, Michael F. Uschold, Christopher A. Welty and David Whitten, with contributions from Mike Genesereth. The ancestor of this entire effort was KIF, authored by Mike Genesereth.
This style indicates notes and comments which are not part of the final text and should not be cited without permission. Some are dated and may have been superceded by others with a later date.
This style indicates text that is likely to change or has been called into question.
LAST POSTED Thursday, May 20, 2004 8:09:36 PM
The syntax has = put back in as a basic syntactic form, and the variadic = has been renamed 'scl:same'. The syntax has been rewritten using real EBNF. The MT now uses two distinct extension mappings for relations and functions, and the old KIF identity is not supported, cf. http://philebus.tamu.edu/pipermail/scl/2004-February/000694.html. The intuitive discussion in the surrounding text has been re-written based on negotations beween alternative conventional interpretations.The terminology of 'fitting conditions' has been removed and replaced with the notion of 'fold'. New figures drawn.
2/15. Some bugs in syntax and text fixed, noted by Mark Stickel. 2/20 Lexical syntax completely rewritten. 2/23 Changes to lexical syntax and character coding text, suggested by Frank Farance.
To do next: discussion and basic lemma on satisfaction; first pass at XML syntax.
3 March. Following suggestions by Mark Stickel, the lexical syntax has been tweaked. Sequence variables now are marked with ellipsis ... rather than @, and the lexicalization is more forgiving of oddities such as names that start with an equality sign.
11 May. NOTE. Robert Kent has developed an IFF-based account
of SCL, with a slightly different semantics; for details see http://suo.ieee.org/IFF/metalevel/lower/namespace/scl/version20040505-obj.pdf
and for background see
http://suo.ieee.org/IFF/metalevel/upper/ontology/multitudes/version20040606.pdf
The core syntax has been modified to allow a form of guarded quantifier. This change is provisional and has not been discussed by the group. 12 May. Error in EBNF corrected (noticed by Dave). 18 May.
*** 20 May. Tanel Tammet has produced a variation which in many ways is simpler than this version. See http://www.ttu.ee/it/elm/ecl.html . I propose to work on merging these as a first priority. This will involve major rewriting and reorganization of the text.
SCL is a first-order logical language intended for information exchange and transmission. SCL allows for a variety of different syntactic forms, called dialects, all expressible within a common XML-based syntax and all sharing a single semantics.
Most of the design aspects of SCL can be understood by considering the following scenario.
Two people, or more generally two agents, A and B, each have a logical formalization of some knowledge. They now wish to communicate their knowledge to a third agent C which will make use of the combined information so as to draw some conclusions. All three agents are using first-order logic, so they should be able to communicate this information fully, so that any inferences which C draws from A's input should also be derivable by A using basic logical principles, and vice versa; and similarly for C and B. The goal of SCL is to provide a logical framework which can support this kind of communication and use without requiring complex negotations between the agents.
This ought to be simple, but in practice there are many barriers to such communication.
First, A and B may have used different surface syntactic forms to express their knowledge. This is a well-known problem and various proposals have been made to solve it, usually by defining a standard syntax into which others can be translated, such as KIF [refKIF]. SCL tackles this issue similarly by providing a common 'interlingua' syntax XCL into which the others can be translated. XCL uses XML concepts and design principles (inspired by MathML 2.0 [refMathML]) to provide a clean separation between the description of logical form and the surface syntactic form appropriate to a particular usage. It also allows for linking of SCL text across documents and conveying SCL written in non-XCL syntaxes between applications using XML protocols.
Second, A and B may have made divergent assumptions about the logical signatures of their formalizations. It is common for one agent to use a relation name for a concept described by another as a function, for example, or for two agents to use the same relation with different argument orderings or even different numbers of arguments. More radically, a particular concept, such as marriage, might be represented by A as an individual, but by B as a relation. Often, one can give mappings between the logical forms of such divergent choices, many of which are widely familiar; but in a conventional first-order framework, these have to be considered meta-mappings which translate between distinct formalizations; and very few general frameworks exist to define such meta-syntactic mappings on a principled basis, in a way that allows reasoning agents to draw appropriate conclusions. This problem has not been so widely recognized or discussed as the first one, but it is ubiquitous. SCL tackles this issue by as far as possible removing the conventional limitations on first-order signatures, allowing apparently divergent styles of formalization to co-exist and the relationships between them to be expressed axiomatically when required. For example, a name in SCL may serve both as an individual name and as a relation name. One of the new aspects of SCL is a formal technique for specifying a coherent first-order semantics for a signature-free logical syntax.
Third, A and B may have been writing with different intended universes of discourse in mind. This kind of situation is quite common: very few ontology composers are able to bear in mind that their assertions might be understood to be talking about things that they have not even conceived of. The results, when formal axioms are combined naively, can be quite unpredictable. If A is thinking about taxonomic classifications of animals, say, it is often difficult to bear in mind that the complement of the set of mammals may be taken by B, and hence by C, to include fruit, sodium molecules, styles of avant-garde paintings or the names of fictional characters in movies. SCL provides a special 'top-level' syntactic form called a module which automatically gives a name to the universe of discourse of a named ontology, and automatically inserts guards on any contained quantifiers when information is combined. This form is optional, to allow for applications where logical sentences are intended to be combined without applying any such transformations; but its use has many incidental advantages for general information exchange on a network, among them being that all such information is automatically expressed in a decideable subcase of first-order logic [refGuardFrag].
SCL also has some other features unusual in a conventional logic but which are intended to facilitate information exchange, including a general technique for using information from externally defined datatypes and databases and a provision for publishing named ontologies for 'public' use on a network.
Historically, the SCL project arose from an effort, called the Common Logic initiative, to update and rationalize the design of KIF [refCL][refKIF], which was first proposed as a 'knowledge interchange format' over a decade ago and, in a simplified form, has become a de facto standard notation in many applications of logic. Several features of SCL, most notably its use of sequence variables, are explicitly borrowed from KIF. However, the design philosophy of SCL differs from that of KIF in various ways, which we briefly review here.
First, the goals of the languages are different. KIF was intended to be a common notation into which a variety of other languages could be translated without loss of meaning. SCL is intended to be used for information interchange over a network, as far as possible without requiring any translation to be done; and when it must be done, SCL provides a single common semantic framework, rather than a syntactically defined interlingua.
Second, largely as a consequence of this, KIF was seen as a 'full' language, containing representative syntax for a wide variety of forms of expressions, including for example quantifier sorting, various definition formats and with a fully expressive meta-language. The goal was to provide a single language into which a wide variety of other languages could be directly mapped. SCL, in contrast, has been deliberately kept 'minimal': the kernel in particular is a tiny language. This makes it easier to state a precise semantics and to place exact bounds on the expressiveness of subsets of the language, and allows extended languages to be defined as encodings of axiomatic theories expressed in SCL, or by reduction to the SCL kernel.
Third, KIF was based explicitly on LISP. KIF syntax was defined to be LISP S-expressions; and LISP-based ideas were incorporated into the semantics of KIF, for example in the way that the semantics of sequence variables were defined. Although the SCL core surface syntax retains a superficially LISP-like appearance in its use of a nested unlabelled parentheses, and could be readily parsed as LISP S-expressions, SCL is not LISP-based and makes no basic assumptions of any LISP structures. The recommended SCL interchange notation is based on XML, a standard which was not available when KIF was originally designed.
Finally, many of the 'new' features of SCL have been motivated directly by the ideas arising from new work on languages for the semantic web [refSW], and in particular, SCL is intended to be useable as a slightly improved Lbase [refLbase], i.e. as serving the role of a semantic reference language for other SW notations.
Perhaps we should leave this until later, since we don't actually do anything about this issue until we introduce XML later in the document.
It is clear that the 'same' logical expression can be rendered in a variety of different syntactic, or even graphical, forms: connectives can be written as infix, postfix or prefix, groupings indicated by brackets, groups of dots or graphically by enclosing circles, etc.. The differences in appearance between surface forms can be quite extreme. A simple logical expression written in introductory text-book form:
(∀x)(Boy(x) → (∃y)(Girl(y) & Kissed(x,y)))
appears in conceptual graph interchange form [ref CGIF] as:
[@every *x] [If: (Boy ?x) [Then: [*y] (Girl ?y) (Kissed ?x ?y) ]]
which is itself a 'linear' rendering of a diagrammatic representation:
@@ insert diagram as figure
Extremely compact notations have been used, such as the postfix convention which requires no parentheses:
KissedxyGirly&EyBoyxIAx
while at the other extreme, this example can be rendered as MathML [refMathML] content markup:
<apply>
<forall/>
<bvar> <ci>x</ci> </bvar>
<apply><implies/>
<apply>
<ci>Boy</ci>
<ci>x</ci>
</apply>
<apply>
<exists/>
<bvar> <ci>y</ci> </bvar>
<apply><and/>
<apply>
<ci>Girl</ci>
<ci>y</ci>
</apply>
<apply>
<ci>Kissed</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>
</apply>
</apply>
</apply>
give example in John's controlled English
To provide for information exchange between such a plethora of syntactic alternatives, SCL follows the lead of the KIF initiative by providing a single 'standard' logical interchange language XCL (based on XML rather than LISP)
Note. There is a divergence of ideas/approaches here. Best thinking is that the XML is the true 'abstract' syntax' for interchange and the core is simply a minimal 'clean' version of the language written using a KIF-style dialect. This will require rewriting this section. Stance wil be: XCL is for interchange, Kernel is for semantic specification and metatheory. XCL is rebarbative and extendable and covers all the syntactic options; Kernel is terse, minimal and easy to parse. Core is a KIF-like compromise for established logic applications, a useable extension to Kernel providing a variety of handy syntax forms. Also note that other dialects can be defined and indeed are encouraged, and XCL provides for their inclusion.
and a general technique for translating other notations, called SCL dialects,
into XCL. One 'human-readable' SCL dialect, the SCL Core syntax, designed
to be similar to KIF syntax, is defined carefully in this document using ENBF,
and is used to give examples. A minimal subset of the
Following KIF, all SCL core expressions consist of a pair of parentheses enclosing
the logical subexpressions of the expression in question, usually with a word
immediately following the opening parenthesis which indicates the logical category
of the expression. Atoms and terms are written in the form
(R a b)R(a b) , and connectives
are written as prefixes rather than infixed. The above example in SCL core syntax
is:
(forall (x) (implies (Boy x) (exists (y) (and (Girl y)(Kissed x y) ))
))
which translates into the SCL kernel form
(forall (x) (not (and (Boy x) (forall (y) (not (and (Girl y)(Kissed x
y) ))) )))
A detailed syntax for SCL Core is given later.
SCL can be expressed a variety of dialects, and this document
defines several which provide SCL variants similar to existing logical notations
in widespread use, and a general XML-based syntax, XCL, for general
purposes of information exchange. XCL allows assertions to declare their dialect,
and so can be used as a general-purpose interchange notation and mark-up language
for any conforming SCL syntax. XCL is also considered to be the definitive 'abstract
syntax' of SCL, in the sense that any language which can be parsed into XCL
so as to preserve its semantic meaning may be considered to be an SCL dialect.
Conventionally, a first-order language is defined relative to a particular signature, which is a lexicon sorted into disjoint sublexica of individual names, relation names and perhaps function names, the latter two each associated with a particular arity, i.e. a fixed number of arguments with which it must be provided. This provides a simple context-free method of checking well-formedness of terms and atomic sentences, and ensures that any expression obtained by substitution of well-formed terms for variables will be assigned a meaningful interpretation.
The notion of signature is appropriate for textbook uses of logic and for stand-alone formalizations: but applied to an interchange situation, where sentences are distributed and transmitted over a network (in particular, on the WWWeb) and may be utilized in ways that are remote from their source, this would require either that a single global convention for signatures be adopted, or else that all communication between agents must involve a negotation about how to translate one signature into another. Both of which are impractical. SCL therefore is designed to have no built-in assumptions about signatures: it allows information to be combined even when it is written using divergent assumptions about the appropriate signature. In fact, there is no notion of signature in SCL syntax: it is replaced with the idea that the semantic role of a name - in fact, of any term - is determined by its syntactic context, that is, by the position it occupies inside another expression. This has a number of consequences for both the syntax and semantics of SCL.
Consider the situation of two agents A and B communicating information to C,
and suppose that there is some concept used by both A and B but with different
signatures. For example, A might use a relation married with two
arguments (the people who are married), while B might use it with three (two
people and a time-interval); or as a function from people to time-intervals.
Cases like this can be handled very simply merely by allowing a symbol to play
more than one role. SCL simply allows relation and function symbols to be variadic,
i.e. to take any number of arguments, and it allows a relation name to be used
as as function name and vice versa. Thinking in traditional terms, this amounts
to allowing a kind of 'punning', often allowed in mechanized inference systems,
where a single name is allowed to play several syntactic (and hence semantic)
roles at once. SCL treats this more simply by conflating the various relational
roles into a single notion of a variadic relation, and similarly for functions.
(SCL modules, described later, allow the user to fix the
arity of any function or relation name if this is required, for example for
purposes of syntactic checking.) Note that this is purely a syntactic
'permission' to use a name in multiple roles: SCL does not assume any particular
relationship between the truth of sentences in which the name plays these various
roles, so for example (R a) neither entails nor is entailed by
(R a b) or (exists (x) (R a x)) or any other sentence
constructed using R with two arguments; and similarly there are
no logical entailments between sentences using R as a relation
and other sentences using R as a function. Such conventions can
be stated as axioms in SCL itself, but the SCL semantics does not impose them
as a matter of logical necessity. Since there are no relevant logical principles
which would mandate any such connection if distinct names were used for the
various signature-distinct cases of the name, this punning does not violate
the 'common logic' principle.
It is also possible that A uses a name such as married as an individual
name while B uses it as a relation name. For example, A might have an ontology
of interpersonal states, perhaps categorized in some way. It is important to
understand that this is not necessarily an irreconcileable difference of opinion
between A and B. The traditional Tarskian semantics for first-order logic requires
that the universe of discourse be a nonempty set of things called 'individuals',
but it does not mandate what kind of things must be in this set. In
particular, there is no requirement that individuals be in any sense inherently
non-relational in nature. Thus, A's use of a name to denote an individual, and
B's use of the same name to denote a relation, need not be considered a difference
of opinion: they can both be right, and can both correctly use first-order reasoning.
In this case, however, the agent C who wishes to make use of both their sentences
is faced with a dilemma, since traditional first-order signature-based syntax
is unable to accomodate both points of view at once. SCL relaxes this rigidity
and allows 'punning' between relation and individual names, as between relation
and function names. In this case, however, the requirement that C must be able
to understand both uses and still be able to reason appropriately has some more
significant consequences. Since A can state equations between individuals and
use terms to denote them, as for example in an equation such as
(= married (conjugalRelationBetween Joe Jane))
our 'common logic' requirement implies that C must be able to reason similarly, even when faced with an expression from B in which the name appears in a relation position:
(married Jack Jill)
The resulting expression has a term in a relation position and would be considered syntactically illegal in most traditional syntaxes for first-order logic:
((conjugalRelationBetween Joe Jane) Jack Jill)
However, it has a perfectly clear first-order reading which can be taken directly
from the conventional readings of the sentences used by A and B, viz.: the relational
entity which is the value of the term (conjugalRelationBetween Joe Jane),
being identical to married, holds true between Jack
and Jill.
Similarly, since A may use existential generalization on this individual name, for example to infer
(exists (x) (= x (conjugalRelationBetween Joe Jane)))
then C must be able to use similar logical inferences on the name, even when it occurs in sentences from B as a relation (or function) name, producing sentences even less conventional when viewed as first-order syntax:
(exists (x) (x Jack Jill))
SCL also allows this as legal syntax.
The resulting syntactic freedom allows a wide variety of alternative first-order axiomatic styles to co-exist within a common syntactic framework, with their meanings related by axioms, all expressed in a single uniform language. For example, the idea of marriage can be rendered in a formal ontology as a binary relation between persons, or a more complex relation between persons, legal or ecclesiastical authorities and times; or as as a legal state which 'obtains', or as a class or category of 'eventualities', or as a kind of event. Much the same factual information can be expressed with any of these ontological options, but resulting in highly divergent signatures in the resulting formal sentences. Rather than requiring that one of these be considered to be correct and the others translated into it by some external syntactic transformation, SCL allows them all to co-exist, with the connections between the various ontological frameworks to be expressed in the logic itself. For example, consider the following sentences (all written in the SCL core syntax):
(married Jack Jill)
(married (roleset: (husband Jack) (wife Jill)))
(exists (x)(and (married x) (= Jack (husband x)) (= Jill (wife x)) ))
(= (when (married Jack Jill)) (hour 3 (pm (thursday (week 12 (year 1997)))))
)
(= (wife (married 32456)) Jill)
(ConjugalStatus married Jack)
((ConjugalStatus Jack) Jill)
These all express similar propositions about a Jack and Jill's being married,
but in widely different ways. The logical name married appears
here as a binary relation between people; a unary property of a state of affairs,
with associated roles and fillers; a three-place relation between two persons
and a time; a function from numbers to individuals; as an individual 'status',
and finally, although not named explicitly, as the value of a function from
persons to predicates on persons. In SCL all these forms can be used at the
same time: the conjunction of the above set of sentences is syntactically correct
SCL.
SCL also allows quantification over relations and functions. SCL syntax accepts
the use of relation-valued functions, and relations applied to other relations,
and so on. The resulting syntax is similar to that of a higher-order logic;
but unlike traditional omega-order HO logic, SCL syntax is completely type-free.
It requires no allocation of higher types to functionals such as ConjugalStatus,
and imposes no type discipline. HOL languages traditionally requires quite elaborate
signatures in order to prohibit 'circular' constructions involving self-application,
such as
(rdfs:Class rdfs:Class)
SCL syntax, in contrast, is obtained from conventional FO syntax by removing signatureal restrictions, so that both SCL atomic sentences and terms can be described uniformly as a term followed by a sequence of argument terms. The above example, which expresses a basic semantic assumption of RDFS [RDFS], is legal (and meaningful) in SCL.
Readers familiar with conventional first-order syntax will recognize that this syntactic freedom is unusual, and may suspect that SCL is a higher-order logic in disguise. However, as has been previously noted on several occasions [ref HILOG][refHenkin?], a superficially 'higher-order' syntax can be given a completely first-order semantics, and SCL indeed has a purely first-order semantics, and satisfies all the usual semantic criteria for a first-order language, such as compactness and the Skolem-Lowenheim property.
What makes a language semantically first-order is the way that its names and quantifiers are interpreted. A first-order interpretation has a single homogenous universe of individuals over which all quantifers range; any expression that can be substituted for a quantified variable is required to denote something in this universe. The only logical requirement on this universe is that is a non-empty set. Relations hold between finite sequences of individuals, and all that can be said about an individual is the relations it takes part in: there is no other structure. Individuals are 'logically atomic' in a first-order language: they have no logically relevant structure other than the relationships in which they participate. Expressed mathematically, a first-order intepretation is a purely relational structure. It is exactly this essential simplicity which gives first-order logic much of its power: it achieves great generality by refusing to countenance any restrictions on what kinds of 'thing' it talks about; it requires only that they stand in relationships to one another.
Contrast this with for example higher-order type theory, which requires an interpretation to be sorted into an infinite heirarchy of types, satisfying very strong conditions. In HOL, a quantification over a higher type is required to be understood as ranging over all possible entities of that type; often an infinite set. The goal of higher-order logic is to express logical truths about the domain of all relations over some basic universe, so a higher-order logic supports the use of comprehension principles which guarantee that relations exist. In contrast, SCL only allows the universe to contain relations, but imposes no conditions on what relations exist other than those required to ensure that every name has a referent.
In FO semantics, a relation name is interpreted as denoting a set of sequences of individuals, being the sequences between which the relation holds: call this a relation set, or a relational extension. In the SCL syntax, the same name might be used to refer to an individual. To retain the essentially first-order nature of the interpretation in cases like this, SCL assumes that a relation name used as an individual name must refer to an individual which, if it is ever called upon the play the role of a relation, is true of exactly the same sequences. The relational individual is 'associated' with same relation set as its name. This ensures that the name retains a single meaning in all contexts of use. The mappings which define such associations between individuals and relational and function extensions are called folds.
The intuition behind this terminology is the sense of 'folding' used in cookery: Merriam-Webster Online Dictionary: fold[3, verb] sense 6: "6 a : to incorporate (a food ingredient) into a mixture by repeated gentle overturnings without stirring or beating; b : to incorporate closely."
Note that we do not assume that the individual denoted by the relation symbol is the relation set itself. While that interpretation might be thought set-theoretically more natural, to require an individual to be a large set containing structures containing other individuals would be a clear violation of the essentially first-order nature of SCL semantics.
This semantic strategy also allows several distinct individuals to be associated with the same relational extension, which provides an extra measure of descriptive flexibility. One can think of a relational individual as a relation in an intensional sense, and a relation set as a relation in a narrower extensional sense. SCL may be said to embody an intensional theory of relations as objects, although the SCL truth-conditions are purely extensional.
Finite sequences play a central role in SCL syntax and semantics. Atomic sentences consist of an application of one term, denoting a relation, to a finite sequence of other terms. Such argument sequences may be empty, but they must be present in the syntax, as an application of a relation term to an empty sequence does not have the same meaning as the relation term alone.
SCL also allows relations to be take any number of arguments: such a relation
is called variadic. (Married is an example of a variadic
relation.) SCL follows KIF also in providing a special syntactic form called
sequence variables to allow generic assertions to be made which apply
to arbitrary argument sequences. Sequence varaibles are indicated in the SCL
core syntax by an ellipsis ... optionally followed by a distinguishing
character string. If an argument sequence ends with a sequence variable, then
the presence of the variable indicates that the sequence may be arbitrarily
extended, and the sentence is required to hold for all the possible extensions.
An SCL axiom using sequence variables can be viewed as a first-order axiom scheme, standing in for a countably infinite set of first-order instances.
Sequence variables are quite a powerful device: in effect, they allow a finite sentence to assert infinitely many quantifications all at the same time. Indeed, if arbitrary quantification over sequence variables is permitted, then the resulting language is a subset of the infinitary logic Lw1w, of a higher expressiveness than first-order logic, and for example is not compact [refHayMenzel]. The restrictions on sequence variables in SCL have been chosen to restrict the language to first-order while providing much of the practical utility of sequence variables for writing 'recursive' axioms to define lists and other recursively defined constructions. In SCL, sequence variables are allowed to occur only in the last position in an argument sequence, and are not bound by quantifiers: this keeps the language first-order and makes term-unification decideable [refKutsia]. Sequence variables can be replaced by a more conventional notation, at some considerable cost in elegance, by introducing argument lists explicitly: we provide a generic header which can be used for this kind of elimination, which is commonly adopted in practical KR notations.
SCL text is any set or sequence of SCL top-level sentences, called SCL phrases.
The SCL core syntax uses sequences throughout, for convenience in defining iterative syntactic operations, but no particular significance attaches to the ordering of the sequence, and other SCL dialects may adopt a set-based syntactic convention.
An SCL module, or simply a module, is some SCL text together with an optional header consisting of SCL text, and which has a global name in the form of a Uniform Resource Identifier [refURI].Headers have a special semantic role and are treated in a distinct way in the semantics: they provide a general method for encoding syntactic and other 'background' information about the module. A special header vocabulary is provided which is sufficient to describe many standard signatures and syntactic conventions; but any SCL text may be included or imported into a header.
The terminology of "text" and "module" is intended to be a neutral terminology used to refer to any coherent piece of SCL which can be published, transmitted or asserted. It is not intended to convey any particular categorization or to indicate an intended use or philosophical stance. Other terms in widespread use in various communities include "ontology", "knowledge base", "axiom set" , "set of sentences", "metadata", "data model" and "model", as well as such particular usages as "RDF graph" and "document".
The core also provides an importing syntax, which indicates that a named module is being included into another module. The intended meanings of these constructions are fairly obvious, but the formal semantic statement requires that we assume the existence of a global module-naming convention, and that module names refer to entities in formal interpretations. This can all be stated abstractly, but is more directly conveyed by the observation that SCL uses the emerging semantic web conventions, as used in RDF and OWL, which are based on the W3C URI naming protocols [ref RFC2396]. The SCL 1.0 importing syntax provides only a very basic functionality for referring to modules, and we anticipate that it will be extended in future versions.
This "top-level" SCL syntax also provides for modules to declare their intended domain of discourse, and other functions intended to be useful in exchanging information.
XCL is SCL in XML. XCL serves three related roles in the SCL project. It is the intended form for interchange of logical content between processors on a network and for machine processing generally; it is the standard 'abstract syntax' for SCL content; and it serves as a reference for other SCL surface syntax forms, known as dialects. XCL has provision for content to be transmitted as dialect text, and also for structured XCL markup to be rendered as dialect text by the use of CSS or XSLT applied directly to the XCL.
XCL markup basics.
The basic design philosophy of XCL is that any logical expression has its syntactic category indicated by an enclosing tag, its textual name rendered as character data, and its subexpressions rendered as child elements. Attributes are used to relate the SCL logical structure to other syntactic categories (such as 'clause' and 'literal') and for various extra-logical purposes. In order to accomodate extensions to the language, 'generic' tags are provided for the main syntactic categories, which can be modified by the "type" attribute.
XCL uses the following tag names:
scl
text
quantifier
forall
exists
boolean
and
or
implies
iff
not
atom
term
name
Time to tackle this!
XCL is an XML notation for SCL designed to serve three inter-related roles. It is the intended interchange language for communicating SCL across a network; it is the primary abstract syntax for SCL into which all other SCL dialects can be translated; and it is a generic notation for incorporating SCL text written in any SCL dialect.
The last of these is the simplest to deal with, so we consider it first. Any piece of SCL text written in any named dialect, treated as XML content and enclosed in an <xcl:text> </xcl:text> element, with the property value of the property scl-dialect identifying the dialect, is a legal XCL element, called a dialect element. Other attributes may be attached to an xcl:text element, but the scl-dialect value is required. Dialect elements allow XCL to transmit SCL text between applications tuned to a particular dialect, with minimal changes to the text.
The name of the core-syntax dialect is coreSyntax. Thus, the following is a legal XCL element:
<xcl:text scl-dialect="coreSyntax">
(forall (x) (implies (Boy x) (exists (y) (and (Girl y)(Kissed x y) )) )) </xcl:text>
Note that this convention assumes that XML escaping is applied
to the enclosed SCL text. For example,
<xcl:text scl-dialect="@@@coreSyntax">
(scl:String 'the use of the less-than character < and the ampersand &
in XML content is forbidden')
</xcl:text>
should be understood as indicating the SCL core syntax expression:
(scl:String 'the use of the less-than character < and the ampersand &
in XML content is forbidden')
There is no XCL requirement that the enclosed SCL dialect text be syntactically well-formed dialect SCL, although applications may report ill-formed dialect SCL as a syntactic error. However, XCL is required to conform to lexical conventions in use, so that if the syntactic specification of a dialect prohibits the use of certain characters or character sequences as lexical items, the use of XML escaping to encode these characters or character sequences is illegal inside an xcl:text element with that dialect property. Such uses must be reported as errors by a conforming XCL application.
For example, this:
<xcl:text scl-dialect="coreSyntax"> (Boy
x shazdam) </xcl:text>
is illegal XCL since the resolved body text:
(Boy x @shaz@am)
cannot be lexicalized in the dialect named.
Should say something about using Xlink to connect pieces of text together into a single text.
SCL can be rendered into XCL directly, in a form which displays the SCL syntax directly in the XML markup. We refer to this as direct XCL markup. This is analogous to "content markup" in MathML [refMathML], and in fact follows the MathML specification closely, and has been designed to allow MathML to be used directly as an XCL element. This is the 'canonical' form of SCL syntax in two senses: it is the recommended form for communicating SCL between processors, and it serves as the definitional target of any SCL dialect. A notation can be called an SCL dialect when it can be encoded into this form, preserving its semantics. Specifications of named SCL dialects must provide an unambiguous specification of a mapping from the dialect syntax into XCL direct markup. The specification may take several forms.
The elements required for the SCL Core are described here, linked to the corresponding clauses of the EBNF SCL core syntax.
Should we think of following MathML in allowing presentation
markup as a way to define a surface syntax?? Or would this be overkill (and
in any case why not just use MathML's own markup??)
Particularly since MathML has some very well-worked-out techniques for linking
presntation markup to structure, using style sheets and so on.
Other SCL dialects may extend these elements with others, provided that the new elements are reducible to the elements given here, in the sense described in section @@@Hmmm, not sure about this. .
The XCL elements are
module
text
phrase
sentence
equation
application
roleatom
term
Example
(forall (x) (implies (Boy x) (exists (y) (and (Girl y)(Kissed x y) ))
))
<scl form="text">
<phrase id="gksjdfgljg" doc="The example used throughout
the SCL primer document">
<quant type="forall"> <var>x</var>
<bool type="implies">
<atom relation="Boy">
<term>x</term>
</atom>
<quant type="exists"> <var>y</var>
<bool type="and">
<atom relation="Girl">
<term>y</term>
</atom>
<atom rel="Kissed">
<term>x</term>
<term>y</term>
</atom>
</bool>
</quant>
</bool>
</quant>
</phrase>
This is no good since it treats relation terms differently than terms in argument position. The syntax has to be uniform. It is hard to avoid the implication that everything is in the body, therefore.
in MathML would be
<apply>
<forall/>
<bvar> <ci>x</ci></bvar>
<apply><implies/>
<apply>
<ci>Boy</ci>
<ci>x</ci>
</apply>
<apply>
<exists>
<bvar> <ci>y</ci></bvar>
<apply><and/>
<apply>
<ci>Girl</ci>
<ci>y</ci>
</apply>
<apply>
<ci>Kissed</ci>
<ci>x</ci>
<ci>y</ci>
</apply>
</apply>
</apply>
</apply>
</apply>
but this seems to suffer from what might be called application-excess, since every SCL syntactic constructor maps into the generic <apply> in MathML, which therefore serves no significant purpose in SCL syntax description. XCL follows this general
The sclmodule element represents a complete SCL module. Normally this will be used only once in a document, and may then be identified by the same URI as the document itself. However, a single document may contain any number of module elements. Following normal WWWeb best practice, every module element must have a unique URI name different from the name of any other module. This is required in order to ensure consistency of the importing mechanism in other modules. The URI of a module should provide an access path to the definition of the module. Typically , the URI of a module in a document will be a URI reference of the form ex:documentURI#moduleName whose base is the URL of the document containing the module definition and whose extension is the internal anchor of the module in that document.
Any module must contain a name in the form of a URI or URI reference and some SCL text. It may also contain a header element.
name
dialect
---------
The SCL Core is the basic 'readable' syntactic form of SCL relative to which the semantics is defined, and which is used to give examples throughout this document. It is not the recommended SCL syntax for information exchange. The choice of syntax for the core is somewhat arbitrary, but was based on KIF for historical legacy reasons and because this form, although slightly unconventional in appearance to an eye accustomed to textbook logical forms, has several advantages for machine processing. The SCL core syntax is not exactly that of KIF 3.0 [refKIF], and it defines a considerably smaller language.
Apart from being a smaller language, SCL Core syntax differs
from KIF in the following respects.
(1) Variables are not required to be marked syntactically, and free variables
are impossible.
(2) .... finish this list later and make it into
an appendix or something: notes for implementers.
FEB 23rd. THE SYNTAX HAS BEEN REWRITTEN. THE LOGICAL SYNTAX IS UNCHANGED BUT THE LEXICAL AND CHARACTER-HANDLING PART IS NEW.
Mar 3. The lexical syntax has been modified yet again.
May 12. The core quanifier syntax has a new option intended to express guarded quantification. This has not yet been fully integrated into the rest of the description of the logic, and may be modified in the future.
Any SCL Core, or core, expression is encoded as a sequence of Unicode characters as defined in ISO/IEC 10646-1. Any character encoding which supports the repertoire of ISO 10646-1 may be used, but UTF-8 (ISO 10646-1:2000 Annex D ) is preferred. Only characters in the US-ASCII subset are reserved for special use in the core itself, so that the language can be encoded as an ASCII text string if required. This document uses the ASCII encoding. Unicode characters outside that range are represented in ASCII text by a character coding sequence of the form \unnnn or \Unnnnnn where n is a hexadecimal digit character. When transforming an ASCII text string to a full-repertoire character encoding, such a sequence should be replaced by the corresponding direct encoding of the character.
Some of these unicode references MAY need checking.
The syntax of the core is designed to be easy to process mechanically and to impose minimal conditions on the character sequences which can be used as logical names. The syntax is defined in terms of disjoint blocks of characters called lexical tokens (in the sense used in ISO/IEC 2382-15). A character stream can be converted into a stream of lexical tokens by a simple process of lexicalisation which checks for a small number of delimiter characters, which indicate the termination of one lexical token and possibly the beginning of the next lexical token. Any consecutive sequence of whitespace characters acts as a separator between lexical tokens. Certain characters are reserved for special use as the first character in a lexical item; in particular, the single-quote (apostrophe U+002C) character is used to start and end quoted strings, which are lexical items which may contain interlexical characters, and the equality sign must be a single lexical item when it is the first character of an item. The use of the characters less-than < (U+003C), greater-than > (U+003C) ampersand & (U+0038) and double-quote " (U+0022) is deprecated, in order to minimise interactions with XML processors of SCL core text.
The backslash \ (reverse solidus U+005C) character is reserved for special use. Followed by the letter u or U and a four- or six-digit hexadecimal code respectively, it is used to transcribe non-ASCII Unicode characters in an ASCII character stream, as explained above. Any string of this form plays the same SCL syntactic role in an ASCII string rendering as a single ordinary character. The combination \' (U+005C, U+002C) is used to encode a single quote inside an SCL quoted string.
The following syntax is written using Extended Backus-Naur Form (EBNF),
as specifed by International
Standard ISO/IEC 14977. Literal chararacters are 'quoted',
sequences of items are separated by commas, | indicates
alternatives, { } indicates any sequence of expressions,
- indicates an exception, [ ]
indicates an optional item, and parentheses ( ) are
used as grouping characters. Productions are terminated with ;.
The syntax is writen to apply to ASCII encodings. It also applies to full Unicode character encodings, with the change noted below to the category nonascii.
The syntax is presented here in two parts. The first deals with parsing character streams into lexical items: the second is the logical syntax of SCL Core, written assuming that lexical items have been isolated from one another by a lexical analyser. This way of presenting the syntax allows the logical form to be stated without complications arising from whitespace handling. A complete EBNF syntax is given in appendix @@@ which can be used as a basis for parsing SCL from a character stream.
white = space U+0020 | tab U+0009 | line U+0010 | page U+0012 | return U+0013 ;
Single quote (apostrophe) is used to delimit quoted strings, which obey special lexicalization rules. Quoted strings are the only SCL lexical items which can contain whitespace and parentheses. Parentheses outside quoted strings are self-delimiting; they are considered to be lexical tokens in their own right. Parentheses are the primary grouping device in SCL core syntax.
open = '('
;
close = ')'
;
stringquote = '''
;
char is all the remaining ASCII non-control characters,
which can all be used to form lexical tokens (with some restrictions based on
the first character of the lexical token). This includes all the alphanumeric
characters.
The characters <, & and ' require the use of XML entity references when
SCL core text is represented as XML content. It is recommended that the characters
> and " are also XML-escaped within XML.
char = digit
| '~' | '!'
| '#' | '$'
| '%' | '^'
| '&' | '*'
| '_' | '+'
| '{' | '}'
| '|' | ':'
| '"' | '<' | '>'
| '?' | '`'
| '-' | '='
| '['
| ']' | '\'
| ';'| ','
| '.' | '/'
| 'A' | 'B'
| 'C' | 'D'
| 'E' | 'F'
| 'G' | 'H'
| 'I' | 'J'
| 'K' | 'L'
| 'M' | 'N'
| 'O' | 'P'
| 'Q' | 'R'
| 'S' | 'T'
| 'U' | 'V'
| 'W' | 'X'
| 'Y' | 'Z'
| 'a' | 'b'
| 'c' | 'd'
| 'e' | 'f'
| 'g' | 'h'
| 'i' | 'j'
| 'k' | 'l'
| 'm' | 'n'
| 'o' | 'p'
| 'q' | 'r'
| 's' | 't'
| 'u' | 'v'
| 'w' | 'x'
| 'y' | 'z'
;
digit =
'0' | '1'
| '2' | '3'
| '4' | '5'
| '6' | '7'
| '8' | '9'
;
hexa = digit
| 'A' |
'B' | 'C'
| 'D' | 'E'
| 'F' | 'a'
| 'b' | 'c'
| 'd' | 'e'
| 'f'
;
Certain
character sequences are used to indicate the presence of a single character.
nonascii is the set of characters or character sequences which indicate
a Unicode character outside the ASCII range.
Note. For input using a full Unicode character encoding,
this production should be ignored and nonascii should be understood
instead to be the set of all non-control characters of Unicode outside the ASCII
range which are supported by the character encoding. The use of the
\uxxxx and \Uxxxxxx sequences in text encoded using a full
Unicode character repertoire is deprecated.
innerquote is used to indicate the presence of a single-quote character
inside a quoted string. A quoted string can contain any character, including
whitespace; however, a single-quote character can occur inside a quoted string
only as part of an innerquote, i.e. when immediately preceded by a
backslash character. The occurrence of a single-quote character in the character
stream of a quoted string marks the end of the quoted string lexical token unless
it is immediately preceded by a backslash character.
nonascii = '\u'
, hexa, hexa,
hexa, hexa
| '\U' , hexa,
hexa, hexa,
hexa, hexa,
hexa ;
innerquote = '\''
;
Sequence variables are a distinctive
syntactic form with a special meaning in SCL. Note that a bare ellipsis '...'
is a sequence variable.
seqvar = '...' ,
{ char }
;
Single quotes are delimiters
for quoted strings. A quoted string denotes the text string inside the quotes,
except that the combination \' indicates the presence of a single quote mark
in the denoted string; and in an ASCII character encoding, the presence of a
nonascii sequence indicates a Unicode character at the position in
the denoted string. Any occurrence of the backslash character \ not immediately
followed by the character ' or u or U simply indicates the backslash character
itself. The combination \u or \U may be the initial part of a nonascii
sequence which indicates a Unicode character in the denoted string, but if not
part of such a sequence then it simply indicates itself. With these conventions,
a quoted string denotes the string enclosed in the quote marks. For example,
the quoted string 'a\(b\'c' denotes the string a\(b'c, and '\'a (b\\\') c \\''
denotes the string: 'a (b\\') c \'.
Quoted strings require a different lexicalization algorithm than other parts
of SCL core text, since parentheses and whitespace do not break a quoted text
stream into lexical tokens.
When SCL Core text is enclosed inside markup which uses character escaping conventions,
the SCL quoted string conventions here described are understood to apply to
the SCL text described or indicated by the conventions in use, which should
be applied first. Thus for example the content of the XML element: <scl-text>'a\'b<c&apos</scl-text>
is the SCL core syntax quoted string 'a\'b<c' which denotes the five-character
text string a'b<c . Considered as bare SCL text, however, 'a\'b<c&apos
would simply be a rather long SCL name.
quotedstring = stringquote, { white | open | close | char | nonascii | innerquote }, stringquote ;
reservedelement consists of the lexical tokens which are used to indicate the syntactic structure of SCL. These may not be used as names in SCL text.
reservedelement = '=' | 'and'
| 'or' | 'iff' | 'implies'
| 'forall' | 'exists' |
'not' | 'roleset:' | 'scl:imports'
| 'scl:header' | 'scl:module'
| 'scl:comment' ;
A namesequence is a lexical token which does not start with any of the special characters. Note that namesequences may not contain whitespace or parentheses, and may not start with a quote mark although they may contain it; and that numerals are syntactically similar to namesequences but are distinguished for semantic reasons.
namesequence = ( char , { char | stringquote } ) - ( reservedelement | numeral | seqvar ) ;
lexbreak = open
| close | white
, { white
} ;
nonlexbreak = numeral
| quotedstring |
seqvar | reservedelement
| namesequence ;
lexicaltoken = open
| close
| nonlexbreak ;
charstream = { white
}, { lexicaltoken,
lexbreak } ;
Lexical tokens are divided into eight mutually disjoint categories: parentheses,
the equality sign, numerals, quoted strings (which begin with '''),
seqvars (which begin with '...'),
reserved elements and namesequences. Lexical tokens other than parentheses are
separated by whitespace or parentheses. Thus, whitespace adjacent to a parenthesis
is optional. The task of a lexical analyser is to parse a character stream as
a charstream, and to deliver the lexical
tokens it finds, in order, to the next stage of parsing.
Note that occurrences of quote marks, equality or ellipses inside
a name sequence lexical token have no particular
lexical significance. However, a string quote or ellipsis initiating
any lexical token requires that the token be parsed
as a quoted string.or a sequence
variable respectively. For example,
' 'a'bc '
is an error (cannot be parsed as a charstream) since
the first single-quote symbol immediately follows a white,
so initiates a quotedstring which is required
to be terminated by the second stringquote, but
there is no lexbreak to separate this from the next
token; but ' a'a'bc '
is a legal name sequence. Any char
string may occur as an internal part of a name sequence
or sequence variable; for example, 'forallIknow
' , 'a=b'
, 'a...b' and
'==>'look_here'<=='
are all name sequences, and '...a',
'...a...',
'.....' and
'...' are all
legal seqvars. Identity of lexical
tokens can be checked by a simple character-by-character string match.
A name is any lexical token which is understood to denote. The expression syntax, below, uses this category; it is not required for lexicalization.
name = namesequence | numeral | quotedstring ;
This part of the syntax is written so as to apply to a sequence of SCL lexical tokens rather than a character stream, so it ignores whitespace handling. A full EBNF syntax for SCL Core suitable for generating parsers of character-level data is given in appendix @@@..
Both terms and atomic sentences use the notion of a sequence of terms representing a vector of arguments to a function or relation.
termseq = { term } , seqvar? ;
Names count as terms, and a complex (application) term consists of a term denoting a function with a vector of arguments. Terms may also have an associated comment in the form of a quoted string. Note that this now requires an explicit comment marker in the core syntax.
term = name
| ( open,
term , termseq,
close ) | ( open,
'scl:comment', quotedstring
, term,
close ) ;
Equations are distinguished as a special category because of their special semantic role and special handling by many applications. Note that the equality sign is not a term.This is a change from the previous version of the syntax.
equation = open,
'=', term,
term, close
Atomic sentences are similar in structure to terms. In addition, equations are considered to be atomic, and an atomic sentence may be represented using role-pairs consisting of a role-name and a term.
atomsent = equation
| ( open, term
, termseq,
close ) | ( open,
term, open,
'roleset:' , { open,
name, term,
close } , close,
close ) ;
Boolean sentences require implication and iff to be binary, but allow and and or to have any number of arguments (including zero).
boolsent = (
open, ('and'
| 'or') , { sentence
}, close ) | ( open,
('implies' | 'iff')
, sentence , sentence,
close ) | ( open,
'not' , sentence,
close ;
Quantifiers may bind any number of variables and may be guarded;
and bound variables may be restricted to a named category.
The guarded-quantifier syntax - the optional name
immediately after the quantifier - is a new option not in the previous version.
May 12.
quantsent = open,
('forall' | 'exists')
, [ name ] , open,
{ name | (
open, name,
term, close
)} , close,
sentence, close
;
Like terms, sentences may have comments attached.
sentence = atomsent
| boolsent | quantsent
| ( open,
'scl:comment', quotedstring
, close )
;
SCL text is a sequence of phrases, each of which is either a 'top-level' sentence, an importation, or a bare comment. We distinguish sentence from phrase because phrases are considered to bind sequence variables. The name argument of an importation will usually be a URI.
phrase = sentence
| open,'scl:imports',
name , close
| open, 'scl:comment',
quotedstring, close
;
scltext = {
phrase } ;
An SCL module is a named piece of text with an optional header containing text which is intended to convey 'meta-information'; details are given later in the document.
moduledefinition =
open, 'scl:module'
, name , [open,
'scl:header' , scltext
, close ]
, scltext , close
;
Specialname is a category of lexical tokens to which SCL attaches particular semantic meanings. Although they are not required to be distinguished for parsing purposes, the list of special forms in the SCL Core syntax is appended here for convenience. Other SCL dialects may extend this category to include other name forms reserved for special use, and headers may declare other classes of special forms. If a special form is used in any SCL text then its meaning as a special form cannot be over-ridden by any other interpretation of that text, so inappropriate uses of special forms may produce inconsistencies.
specialname = 'scl:same'
| 'scl:different' | 'scl:arity'
| 'scl:Ind' | 'scl:Rel'
| 'scl:Fun' | 'scl:Integer'
| 'scl:String' | numeral
| quotedstring;
It is useful to distinguish a subset of the core syntax which is just sufficient to define the meanings of all the other logical constructions. The semantics will be defined on this minimal 'kernel', and the meanings of the remaining constructions defined by a systematic translation to the kernel.
The kernel syntax omits the role-pair syntax for atomic sentences, restricted
quantification, the existential quantifier and all connectives other than and
and not, and it does not support the module syntax, but is restricted
to simple SCL text. Terms, term sequences
and equations are identical to the core syntax, and
the breakdown of the sentence category into four types is identical to that
used in the core.
atomsent = equation
| open, term,
termseq, close
; compare core atomsent
boolsent =
open, 'and'
, { sentence },
close | open,
'not' , sentence
, close ; compare
core boolsent
quantsent =
open, 'forall'
, open, name
, close, sentence
, close ;
compare core quantsent
sentence =
atomsent | boolsent
| quantsent ;
same subdivision into sentence categories as core
phrase = sentence
; compare core phrase
scltext = { phrase
} ;
The translations of the other core expression patterns into the kernel are
given by the following table. The first line defines the meaning of role-set
atoms, discussed in more detail above: the variable x introduced
in this line is assumed to be distinct from any other names occurring in the
expression. The remaining translations are the standard textbook reductions
of logical expressions to the forall-and-not subcase. Need
to add a translation for guarded quantifiers
| expression E of type | with syntactic form | translates to kernel expression K[E] |
| atomsent | (t (roleset: (n1 t1) ... (nm tm))) |
K[ (exists (x) (and (t x) (= t1 (n1
x)) ... (= tm (nm x)) )) ] |
| boolsent | (or s1 ... sn) |
(not (and (not K[s1]) ...
(not K[sn]) )) |
(implies s1 s2) |
(not (and K[s1] (not K[s2])
)) |
|
(iff s1 s2) |
(and K[ (implies s1 s2) ] K[
(implies s2 s1) ] ) |
|
| quantsent | (forall g (...) s) |
K[ (forall (...) K[
(implies (g <free> ) s )) ] ] DAMN
this is very hard to describe recursively. Maybe I'll have to resort to
text. |
(forall ((x t) ...) s) |
(forall (x) K[(forall (...) s) ))) ] |
|
(forall (x ...) s) |
(forall (x) K[ (forall (...)
s) ] ) |
|
(forall () s) |
K[ s ] |
|
(exists (...) s) |
(not K[ (forall (...) (not K[
s ])) ] |
|
| sentence | (scl:comment 'string' s) |
K[ s ] |
The earlier example
(forall (x) (implies (Boy x) (exists (y) (and (Girl y)(Kissed x y) ))
))
can also be expressed in the core syntax by using quantifier restrictions:
(forall ((x Boy)) (exists ((y Girl)) (Kissed x y) ))
Both translate into the SCL kernel form:
(forall (x) (not (and (Boy x) (forall (y) (not (and (Girl y)(Kissed x
y) ))) )))
Note that comments, 'vacuous' quantifiers which do not bind a variable, comments and
Several special cases of the kernel syntax can be identified, largely by restrictions on the syntax of atomic sentences and terms.
Text is first-order if it contains no sequence variables, the only terms which occur in relation or function positions are names, and every name occurs in only one kind of position. If no term occurs in function or relation position in two atoms or terms with different numbers of arguments, then the text is fixed-arity. Fixed-arity first-order text corresponds to the traditional notion of a first-order signature: the names in the vocabulary can be subdivided into relation, function and individual names, each occurring only in its alloted role in the syntax, and with each function or relation having a fixed number of arguments. We will refer to this case as goffol text.
If all terms are names, so there are no expressions in function position, the text is pure relational.
If no variable occurs in any term in function position, then
the text is rigid. Rigid text represents a useful compromise between
the syntactic freedom of general SCL and the syntactic predictability of goffol
syntax. Notice that rigidity only restricts the occurrence of variables inside
terms in function position: rigid text allows arbitrary terms to occur in relation
position, and names in relation position may be bound by quantifiers.
Its probably no longer worth distinguishing this case, unless it shows up naturally in the metatheory.
This means that the content of a non-rigid text can often
be expressed in equivalent rigid text by unpacking all the non-rigid terms and
replacing them with suitable relational atoms, for example by re-writing
(forall (x y)( (R ((f y) x)) ... ))as
(forall (x y) (exists (z) (and (f z y) (functional f) ( (R
(z x)) ... ))))
with the additional axiom:
(forall (f) (iff (functional f) (forall (x y)(implies (and (f x ...)(f
y ...)) (= x y)))))
Apart from the top-level syntax for defining headers and ontologies, the only unconventional aspects of SCL are the syntax for atomic sentences and terms, which reflect the type-free catholicity imposed by the need to allow multiple lexical perspectives to co-exist. This section discusses these features in more detail.
Need a section commenting on the lexical freedom in eg allowing numerals and strings to be relations.
A sequence variable stands for an 'arbitrary' sequence of arguments. Since sequence variables are implicitly universally quantified, any top-level expression in which a sequence variable occurs has the same semantic import as the countably infinite conjunction of all the expressions obtained by replacing the sequence variable by a finite sequence of variables, all universally quantified at the top (phrase) level. For example, the top-level sentence
(R ...)
has the same meaning as the infinite conjunction:
(and...
(R)
(forall (x)(R x))
(forall (x y)(R x y))
(forall (x y z)(R x y z))
)
This includes the 'trivial' case for zero arguments:
(forall ( ) (R))
where the vacuous quantifier is omitted. To omit this case, write the top-level
atomic sentence with one quantified variable and a sequence variable:
(forall (x)(R x ...))
Sequence variables can be used to write 'recursive' axiom schemes. Rather than attempt a fully general description of this technique, we will illustrate it with a canonical example. Consider the following sentences:
(= nil (list))
(forall (x z) (iff (= x (list ...) (= (cons z x) (list z ...)))
which have the same meaning as the infinite set of sentences:
(= nil (list))...
(forall (x z) (iff (= x (list) (= (cons z x) (list z))))
(forall (x z x1) (iff (= x (list x1)) (= (cons z x) (list z x1)) ))
(forall (x z x1 x2) (iff (= x (list x1 x2)) (= (cons z x) (list z x1 x2)) ))
(forall (x z x1 x2 x3) (iff (= x (list x1 x2 x3)) (= (cons z x) (list z x1 x2
x3)) ))
...
(forall (x z x1 x2 xn) (iff (= x (list x1 ...
xn) (= (cons z x) (list z x1 ... xn)) ))...
)
which clearly entails for any finite sequence t1 ... tn
of terms, that
(= (cons t1 (cons t2 (cons ... (cons tn nil) ...
))) (list t1 ... tn) )
and thus provides the familiar LISP technique of writing a sequence of items as a cons-nil list, used more recently as the RDF 'collection' vocabulary [refRDF]. The tail-recursion represented by the axiom is re-expressed here as induction on the length of a proof.
SCL sequence variables do not actually provide a true recursive definition, as the 'schema' can be used only as a source of assertions and cannot itself be derived by using an inductive argument. The more powerful language obtained by allowing sequence variables to be bound by sequence quantifiers does provide true recursive powers, and is therefore in a higher expressive class than any first-order language. For example, it is not compact. A more tractable language can probably be obtained by adding an explicit 'least fixed point' operator, as in the mu-calculus, but this idea goes beyond the scope of this document.
This general technique of imitating tail-recursive definitions by writing them as implications using sequence variables was pioneered by KIF [refKIF] and is one of the primary uses for sequence variables in SCL. What this construction shows, however, is that the use of sequence variables can be replaced, when required, by the use of explicit cons-nil lists as arguments, represented in SCL by nested terms. This convention is widely used in logic programming applications, and in RDF and OWL. The general rule can itself be stated in SCL by using a sequence variable:
(forall (x) (iff (x ...) (x (list ...)) ))
This thus provides a general technique for replacing the use of sequence variables by explicit quantification over argument lists. The costs of this translation are a considerable reduction in syntactic clarity and readability, and the need to allow lists as entities in the universe of discourse. The advantage is the ability of rendering arbitrary argument sequences using only a small number of primitives with a fixed, low arity. SCL can use either convention or both together, and can describe the relationship between them.
Atomic sentences which use the roleset: construction, for example
(Married (roleset: (wife Jill) (husband Jack)))
are considered to take a set of arguments in the form of role-value pairs. In this role-set syntax, the connection between the relation and its arguments is indicated by the role labels rather than by position in an argument sequence, which avoids the necessity of remembering the argument order when writing sentences, and provides some insurance against communication errors arising from sentences using different argument-order conventions.
In SCL, the roles are considered to be binary relations between an entity to which the main predicate applies and the argument, so for example the above atom is equivalent to the existential conjunction:
(exists (x) (and (Married x) (= Jack (husband x)) (= Jill (wife x)) ))
where x indicates an entity which has been variously called an
eventuality, fact, situation, event, state or trope,
and might be rendered in English as "Jack and Jill's being married"
or "the state of marriage between Jack and Jill". For SCL purposes
however it is possible to think of x more prosaically as being
a vector or sequence of arguments, and the role-names as selectors on the elements
of this sequence.
This syntax allows arguments to be provided in a piecemeal
fashion, and allows arguments to be omitted: such arguments are implicitly existentially
quantified. In fact, any such atom entails a similar atom with some of the role-pairs
omitted. Notice the difference in meaning between Married, (Married)
and (Married (roleset:)). The first is a term which denotes
the relational entity and makes no assertion. The second is an atomic sentence
which asserts positively that Married is true of the empty sequence
- probably false in the actual world - while the third, also an atomic sentence,
merely asserts that Married is true of something, to which other
things may be related by unknown roles: in effect, it asserts that a marriage
exists, and so is true in the actual world.
This role-set convention does not itself specify any relationship between the same fact expressed as a role set and by using an argument sequence, but since SCL allows variadic relations, it is possible to use the same relation in both ways, and they can be related axiomatically. For example,
(forall (x y) (iff (Married x y) (exists (z) (and (Married
z) (= x (wife z)) (= y (husband z))) ))
indicates the convention by which a wife must be the first argument of a marriage. Again, SCL provides for both kinds of syntax, separately or together, and can describe a relationship between them using SCL axioms.
It might be worth extending the notion of vocabulary to terms, and then the folds are natural extensions of the interpretation mappings. We need rel(t) becasue of t's position and so if we have int(t) we assign relation(int(t)) and define relation(t) = relation(int(t)). The only part of this that is a at all creative is the assignment, and that comes from B's interpretation.
Terms which occur in SCL text are required to play various semantic roles depending on the position in which they occur. This generalizes the usual notions of signature category for relation, function and individual names. If any term occurs in more than one position then it must be interpretable in several ways. In this section we define these positional notions, which are understood to be relative to a text.
Any term which occurs as the first term in any atomic sentence, or as the first item in a role pair, or paired with a bound variable in a quantifier, is said to occur in relation position. Terms in relation position must be interpretable as designating a relation.
Any term t which occurs as the first term in any other term of the
form (t t1 ... tn) is said
to occur in function position on n; if it is the first term in another
term of the form (t t1 ... tn ...x)
ending with a sequence variable then it is said to occur in function position
above n, or equivalently to occur in function position on m for
all m>=n; and if it occurs as the first item in a role
pair then it is in function position on 1. Terms in these positions are required
to be interpretable as designating functions with the appropriate arity or arities.
Any name occurring as an argument of any other term or atom, or as the second item in a role pair, and any term other than a name, is said to be in object position, or to be a denoting term. Denoting terms are required to denote an individual in the domain of an interpretation.
The only terms which are not denoting terms in an expression are names which occur only in a function or relation position in that expression. Such names are not required to denote individuals (although in the SCL semantics, they may do so, allowing other pieces of text to be consistently added).
For example, in the following text (which is not intended to be particularly meaningful):
(iff (forall (x) (= (f (f x)) (f x)) ) (g f))
((f a) ((f a) a ...))
(R (roleset: (a b)))
the terms f, x, a, (f x),
(f a) , (f (f x)) , ((f a) a ...) and b
are all denoting terms; the terms g, R and (f
a) all occur in relation position; f and a
occur in function position on 1 while (f a) occurs in function
position above 1. In this text, the term (f a) plays three distinct
roles and the names a and f each play two roles. In
contrast, b is only a denoting term and g and R
occur only in relation position.
Clearly, if a term occurs in a position in a text then it also occurs in that position in any larger text. Concatenating two pieces of SCL text may therefore cause a term occurring in either one of them to be required to play more roles in the combined text.
The semantics of SCL is defined conventionally in terms of a satisfaction relation between SCL text and structures called interpretations. For SCL however the interpretations are required to extend the relational and function mappings into the domain so as to provide an appropriate relational interpretation for every individual which may be denoted by a term in a relation or function position. As discussed earlier, this generalizes the usual idea of an interpretation being defined on a fixed signature. In effect, this restricts interpretations to be those which would fit any signature under which the text could be considered to be syntactically legal.
Let T be an SCL text, VO(T) be the set of names occurring in object position in T , VR(T) be the set of names occurring in relation position in T, and VF(T) those occurring in function position in T; called respectively the object, relation and function vocabularies of T. Note that SCL syntax does not require that these vocabularies are mutually exclusive.
Define a relational extension over S to be any set of finite sequences of elements of S, and a functional extension over S to be any set of pairs <s, x> where s is a sequence of elements of S and x is an element of S, such that if <s, x> and <s, y> are in the set then x = y. Say that a functional extension is total on n if it contains a pair <s, x> for every sequence s of length n over S. Note that a functional extension may be total on several n, and may be total on n but not on m.
A bare interpretation of a vocabulary (VO,VR,VF) is defined by a set and three mappings:
A nonempty set UI called the universe;
A mapping intI from VO to UI;
A mapping relI from VR to the set RelI of relational extensions over UI
A mapping funI from VF to the set FunI of functional extensions over UI.
This is a conventional first-order interpretation structure, slightly generalized to allow variadic relations. Note however that SCL does not require that these various lexical categories be distinct.
It is conventional to also require that funI is total on the arity of any function name. This follows in our case from the 'folding conditions' defined below.
SCL syntax allows expressions in which a term other than a name, or a term containing variables, occurs in a relation or function position. In these cases, we will assume that the individual denoted by the term plays the appropriate role of a relation or function required by the syntactic position of the term. This requires extending the rel and fun mappings defined on the vocabulary by adding partial mappings from the universe to the appropriate extensions.
A folded interpretation, or simply an interpretation, of T is a bare interpretation I of T together with two partial mappings relationI and functionI, called fold maps, from UI to relational and functional extensions over UI respectively, which satisfy the conditions described below. In fact it is convenient to extend these mappings to include the interpretation mappings relI and funI on names, so we will define relationI to be a mapping from (RI union VR(T) ) to RelI and functionI a mapping from (FI union VF(T) ) to FunI , where RI and FI are subsets of UI
First, we require that folds respect both the individual and relational parts of the interpretation mappings wherever they overlap, and that when an individual name is also required to play a relational or functional role, that the appropriate extensions are associated with the denoted individual:
if relI(x) is defined then relationI(x) = relI(x); and if intI(x) is defined then relationI(intI(x)) = relationI(x);
if funI(x) is defined then functionI(x) = funI(x); and if intI(x) is defined then functionI(intI(x)) = functionI(x).
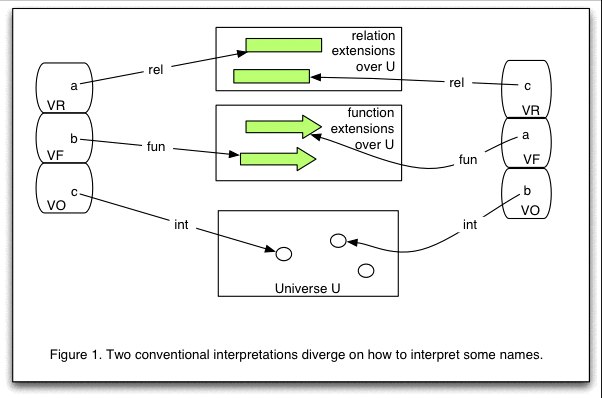
Intuitively, this can be seen as a 'folding' of conditions arising from the disparate requirements of two (or more) conventional interpretations represented by the several basic mappings, as illustrated by the figures below:

To combine these interpretations we simply merge relational extensions mapped from the same name, and similarly for functional extensions; note that the union of functional extensions defined on n and on m is itself defined on both n and m. If a name is required to identify both a relational and a functional extension then it can continue to play both roles. In cases where a name is required to map both to an extension and to an individual, however, we add a fold to associate the individual to the extension:
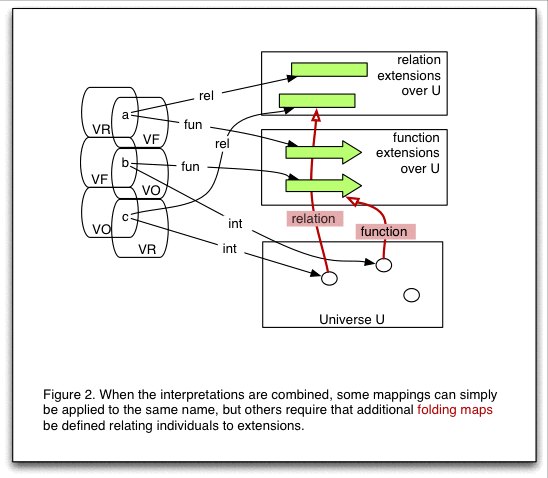
The effect of the fold maps is to ensure that the relational or functional extension identified by the name directly is the same as that identified by the name via its interpretation as denoting an individual. The further conditions described below follow this identification through the syntactic truth-recursions so as to guarantee that any term which occurs in multiple positions will always identify an extension appropriate to the position. This ensures that an interpretation will provide meaningful denotations for all possible expressions which can arise as a result of performing any first-order reasoning process on the text, such as variable instantiation and equality substitution.
It would be possible to define interpretations more simply, but less conventionally, by assuming that all names denote individuals, and associating every individual with both a relational and a functional extension. This obviates the need to consider 'folding' as a special construct and eliminates the need to state recursive conditions on the fold mappings. In many ways the resulting semantic framework, described in [refCLAS], is simpler and more elegant than the one described here; but this version has the advantage of reducing to the conventional Tarskian notion whenever the text fits the traditional syntactic form, so is more clearly a genuine generalization of conventional FO logical semantics. One might call the alternative version a 'maximally' folded semantics, while the current one is 'minimally' folded.
Define a name map on a set S of names to be any mapping from S to UI, and a sequence map to be any mapping from sequence variables to finite sequences of elements of UI. If A is a name or sequence map on S, define IA to be the interpretation which is like A on names or sequence variables in S, but otherwise is like I: formally, UIA = UI, relationIA = relationI, functionIA = functionI, and intIA(v) = A(v) when v is in S, otherwise intIA(v)= intI(v).
When A is a sequence map, this is a slight extension of the notion of interpretation. We use this to provide an interpretation of phrases containing sequence variables. The rest of the truth-conditions map transparently to this extension.
This notation associates to the left, so that IAB = (IA)B, meaning that if
x is in the domain of B then intIAB(x)=B(x). In addition,
we use the following notation: if s= <s1,...,sn> and t=<t1,....,tm>
are finite sequences, then s;t is the concatenated sequence <s1,...,sn,t1,...,tm>
The interpretation I(E) of any SCL core expression E, and the further conditions on the fold maps, are then combined in the following table. An empty cell in the third column indicates that an expression of that type introduces no extra conditions, other than those that arise from its subexpressions.
| SCL interpretation I of an expression E | |||
| if E is a | of the form | then I is an interpretation of E if | and I(E) = |
| name | numeral n |
intI(n) = the decimal value of n |
|
quoted string 'string' |
intI('string') = string
with every innerquote substring replaced by
a single quote character ''' |
||
name, in object position |
intI(name) |
||
name, in relation position |
relationI( and if I( |
||
name, in function position |
functionI( and if I( |
||
| term sequence | (t1 ... tn) |
<I(t1),..., I(tn)> |
|
(t1 ... tn @v) |
<I(t1),..., I(tn)> ; I(@v) |
||
| term | (f seq) |
functionI( |
x, where functionI(f) contains < I(seq),
x > |
(scl:comment 'string' term) |
I(term) |
||
| atom | (= t1 t2) |
true if I(t1)= I(t2), otherwise false. |
|
(r seq) |
If I(r) is defined then I(r) is in RI
andrelationI( r) = relationI(I(r)). |
true if relationI(r) contains I(seq),
otherwise false |
|
| booleanSentence | (not s) |
true if I(s) = false, otherwise false |
|
(and s1 ... sn) |
true if I(s1) = ... = I(sn) = true, otherwise
false |
||
(or s1 ... sn) |
false if I(s1) = ... = I(sn) = false, otherwise
true |
||
(implies s1 s2) |
false if I(s1) = true and I(s2) = false, otherwise
true |
||
(iff s1 s2) |
true if I(s1) = I(s2), otherwise false |
||
| quantifiedSentence | (forall (var) body) |
for any name map B on {var}, IB is an interpretation
of every atom and term in body |
if for every name map B on {var}, IB(body) =
true, then true; otherwise, false. |
(exists (var) body) |
if for some name map B on {var}, IB(body) =
true, then true; otherwise, false. |
||
(forall ((var t) body) |
for any name map B on {var}, IB is an interpretation
of every atom and term in body and of (t var) |
if for every name map B on {var}such that relationI(t)
contains <B(var)>, IB(body) = true, then
true; otherwise, false. |
|
(exists ((var t) body) |
if for some name map B on {var}such that relationI(t)
contains <B(var)>, IB(body) = true, then
true; otherwise, false. |
||
| sentence | (scl:comment 'string' sentence) |
I(sentence) |
|
| phrase | (scl:comment 'string') |
true |
|
sentence |
for any sequence map A on the seqvars in sentence, IA is
an interpretation of every atom and term in sentence. |
if for every sequence map A on the seqvars in |
|
(scl:imports name) |
I is an interpretation of I(name) |
false if I(I(name)) = false, otherwise true |
|
| scltext | s1 ... sn |
I is an interpretation of all of s1 ... sn |
true if I( |
If T is a text and I is a bare interpretation of the vocabulary of T, then any folded interpretation J= (I, relationJ, functionJ) which satisfies the conditions in the third column of the above table is a legal interpretation of T: we will call any such interpretation a folding of I. The conditions in the third column of the semantic table guarantee that all SCL terms will have a unique denotation in any interpretation.
The above differs somewhat from a conventional semantic recursion, in which a bare interpretation is sufficient to determine the semantic values of all expressions. In our case, the syntax of the text also provides a guide to how part of the interpretation must be constructed.
The conditions in the third column in effect extend the basic folding maps from simple names to all expressions and all possible interpretational modifications which arise from the use of quantifiers. To see the effect of these conditions, consider the atomic sentence
((f a) b c)
Here, the term (f a) is required to denote something in the universe
but it is also required to play a relational role. Following down the recursions,
relationI( (f a)) must be defined, and since
I((f a)) - that is, the individual x with <<I(a)>,x
> in functionI(f) - is defined,
the folding map is required to apply to this individual, so that relationI((f
a)) = relationI(I( (f a) )). This ensures
for example that if we also have the equation
(= (f a) foo)
then the result of performing equality substitution preserves the relational interpretation of the term when substituted into a relational position:
(foo b c)
since by virtue of the truth of the equation, I(foo)) = I( (f
a) ); so relationI(foo) = relationI(I(foo))
= relationI(I( (f a) )) = relationI((f
a)). Similar reasoning shows that the substitution of equated names occurring
in functional positions preserves the functional meaning.
Note that the equational rules applied to this text:
(= thisfun thatfun) (P (thisfun a)) (Q (thatfun a b))
requires that there is an individual x = I(thisfun) = I(thatfun)
with functionI(x) total on both 1 and 2. The use of a sequence
variable in a term requires that the function name used in that term have an
associated functional extension which is total on the length of the argument
sequence and every higher number; for example:
(P (f a b ...x))
can only be legally interpreted by an I with relI(f)
total on n for every n greater than or equal to 2.
The presence of a variable in a relation position, for example
(forall (R) (iff (transitive R) (forall (x y z)(implies (and (R x y)(R
y z))(R x z))) ))
requires that the fold map relationI is defined on the entire universe of any interpretation.
To see why, observe that R occurs in relation
position so relI(R) is defined; now choose
some x in UI and consider the variable map A with A(R)
= x, so IA(R) = x. IA is required to be an interpretation of the
body
(iff (transitive R) (forall (x y z)(implies (and (R x y)(R y z))(R x z))) )
(R x y) and hence of the name R
occurring in relation position; and since IA(R) exists, relationIA(x)
must be defined: but this is relationI(x), by
definition of IA.
However, this is in fact a trivial requirement, since one can simply define relationI(x) = { } for all x to which no stronger constraint applies. The strongest possible requirements on a fold arise when a term with a variable in function position also contains a sequence variable, for example:
(forall (f)(implies (functional f) (f (f ...x) ...x) ))
which is equivalent in meaning to the infinite conjunction
(and ...
(forall (f x)(implies (functional f) (f (f x) x) ))
(forall (f x y)(implies (functional f) (f (f x y) x y) ))
(forall (f x y z)(implies (functional f) (f (f x y z) x y z) ))
)
This requires that any legal interpretation I provides a fold mapping functionI which is defined on the entire universe and every value of which is a total function for any number of arguments. However, this too can always be trivially satisfied, for example, by choosing a universal functional value c in the universe and defining functionI(x) to be the set {<s,c> : s a finite sequence }, for all x in T to which no other constraints apply.
In many cases, the fold conditions can be understood as a recursive extension of the basic intepretation mappings on names. Not all pieces of SCL syntax support such a recursive interpretation, however. For example, consider the atomic sentence
(((f a) a) a)
in which f and (f a) both occur in function
position, ((f a) a) in relation position and a
in object position (three times). A bare intepretation I of this vocabulary
provides a universe UI containing at least an individual I(a)
= intI(a) - call it x - and a function extension
funI(f) which is total on UI, so
I((f a)) must be defined: call it y. The fold conditions require
y to be in FI so that functionI((f a))
is defined and is identical to functionI(I((f a))),
ie to functionI(y), and this also is total on UI
, so has a value for the argument intI(a);
this value is I(((f a) a)) - call it z - which is required
to be in RI and so to have a corresponding relational extension relationI(((f a) a)):
and the atom is true when that extension contains <I(a)>.
The process is illustrated in figure 3:
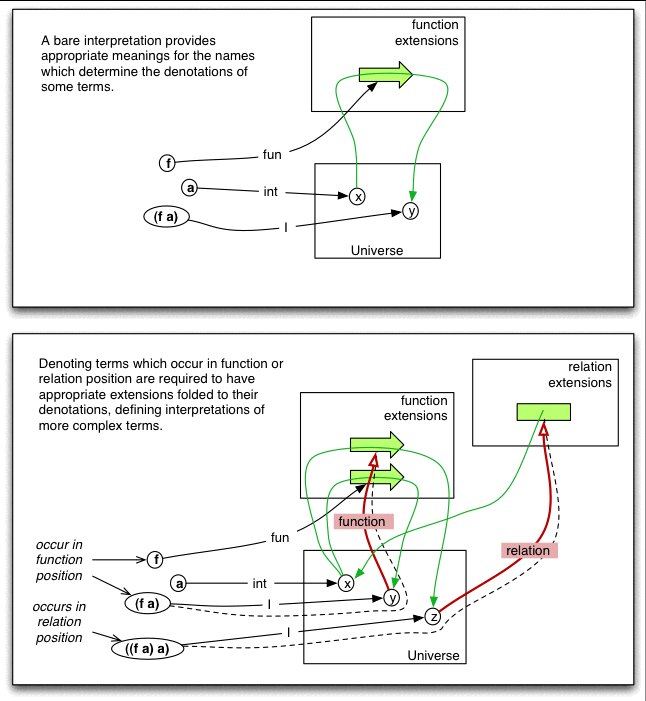
In this case, the folding maps themselves require functional and relational extensions to exist which are not denoted directly by any name in the vocabulary, but are required in order to coherently interpret terms containing other terms in function or relation position. As the example also shows, it is possible for syntactically legal SCL terms to denote individuals which are not present in a bare interpretation of the vocabulary; that is, the fold maps may require the universe of a bare interpretation to be extended. This case will arise only when a complex term occurs in a function position but is not an argument of any other term or atom.
These conditions apply to all interpretations, not just to those which satisfy the text. A structure which fails to satisfy these conditions might fail to provide denotations for some expressions, or fail to assign a truth-value to some sentences. One way to think about these conditions is that they are in a sense the minimal outcome of a process of negotation concerning the appropriate signature role of a name or expression. Suppose two agents A and B are negotiating about the denotation of a name: A wishes it to denote something in the universe of discourse, while B wishes it to play the role of a relation: c.f. figure 1, above. They can both be satisfied if the entity that A takes to be the denotation is allowed to play the role of a relation when the name denoting it occurs in a relation position, and if the relational extension it uses in that role is identical to the relation denoted by the name: for then, all the relational assertions that B wishes to hold will be preserved. Thus, A and B can agree. The conditions on relationI and functionI are the result of following this hypothetical negotiation through the recursions defined by the syntax, in order to ensure that A and B can both assign a meaningful and mutually acceptable interpretation to every possible instance of every expression which can arise from any process of inference applied to their combined texts. In some cases, such as the previous example, this negotiation might require A and B to agree on aspects of an interpretation which do not arise from either of their preferred interpretations taken in isolation, but are imposed on the folded settlement by the syntactic requirements of the language.
Note that this hypothetical negotiation does not require
that any items be added or removed from the universe, or changes made to the
basic interpretation mappings intI, relI
and funI; it is wholly concerned with the appropriate adjustments
to the folding mappings. The above discussion shows that A and B can always
reach an agreement without changing the basic interpretation structure of I.
This needs to be stated more carefully. There
are cases where the universe neds to be enlarged, as in the Horrocks sentences.
HMMM, Im not so sure that this ever does happen in
fact. Anything in the folded interpretation will be in ONE of the universes.
There ought to be a provable result here, that any folded interpretation can
be got by adding extensions and folds to a bare interpretation of the same text,
without extending the universe. Even in the fig3 example, all the terms a (f
a) and ((f a) a) are required to denote simply because they are terms, no matter
what position they are in (??).
What is odd about this example is that it seems to have pieces missing. How could that atom arise from negotiation? Only way I can see is that it could be an equality substitution from (= R (f a)) folding with (R a), but then the R-thing would be in the universe already. We don't have it in our universe because we forgot to mention R explicitly. There is an implicit assumption of monotonicity (!) in this example, therefore, if it is to be motivated by the negotiation discussion. Hmm, interesting.
This construction may place additional requirements on the interpretation,
so it is possible that a bare interpretation of the vocabulary of T may be insufficient
to provide a basis for a suitable folding. In such a case the universe of I
may need to be extended to provide enough distinct individuals to 'carry' the
needed extensions. The construction in the third column of the semantic table
is therefore both part of the definition of a folded interpretation and acts
as a filter on bare interpretations, ruling out those that are too small to
satisfy the text. Thus, a bare interpretation of the vocabulary of T may not
be an interpretation of T.
Consider the notion of shrinking/expansion needed for the header stuff. This seems to apply here too. Then the result would be, given any bare interpr I of vocab(T), there is a J, a folding of an expansion of I which is an interpretation of T. That seems plausible and ought to be easy to prove by an induction on the syntax where J gets built by adding extensions and extending the universe where required.
It would be nice to be able to exactly characterize the conditions that require the universe to be extended. The example in fig 3 is one case, where a term occurs only in relation position. Are all cases like this? No, think of the case of (not (Thing foo)) in a header. Hmmm, maybe we should just make it illegal to use Thing inside a body text (??).
In addition to the basic semantic conditions, interpretations are required to satisfy constraints on the interpretations of the SCL special names, summarized in the following table.
| Special name | satisfies condition |
scl:same |
relI(scl:same) = {<x, ..., x>:
x in UI } |
scl:different |
relI(scl:different) = {<x1,
..., xn>: x1,...,xn all in UI
and xi =/= xj for 1<= i,j <=n} |
scl:Integer |
relI(scl:Integer) = {<n>: n an
non-negative integer in UI} |
scl:String |
relI(scl:String) = {<u>: u a Unicode
character string in UI} |
scl:Thing |
relI(scl:Thing) ={<x1,...,
xn> : x1,...,xn all in UI
}This may need to be changed to allow for named
UODs |
scl:Rel |
relI(scl:Rel) = {<x1, ...,
xn>: x1,..., xn all in RI
} |
scl:Fun |
relI(scl:Fun) = {<x1, ...,
xn>: x1,..., xn all in FI
} |
scl:arity |
relI(scl:arity) = |
All SCL dialects and extensions are required to satisfy these general conditions. Other SCL dialects and extensions may also impose semantic conditions on other categories of special names; some examples are given later.
scl:same and scl:different are convenient abbreviations
for conjunctions of n equations and n(n-1) negated equations respectively, where
n is the number of arguments.
Note that scl:different is identical in meaning
to the negation of scl:same only in the case where both
are applied to precisely two arguments.
The conventions for strings and numerals can be viewed as special 'built-in' datatypes, following the datatype convention described below: the other items are special vocabulary primarily intended for use in module headers, also described later.
@@@@@@@@@@@@@@@@@@@@@@@
----------------@@@@@@@--------------
Say that an interpretation I satisfies an SCL text T when I is an interpretation of T and I(T)=true.
If I is a bare interpretation of the vocabulary of T then say that I satisfies T if there is a folding (I, rI, fI) which satisfies T. Note that this is a requirement on I itself: in effect, it requires I to provide enough individuals and appropriate extensions sufficient to enable a suitable folding to be built on the foundation provided by the bare interpretation.
Need show that if I is a bareinterp of V containing vocab(T) and vocab(S) and I satisfies T and S, then it satisfies T+S. The idea is to combine the folding conditions: need to show it can always be done so as to preserve satisfiability. This ought to be pretty trivial but does requirte an induction. Right now I need to go to bed.
This is the core point about folding: adding new vocabulary can always be handled by adding folds.
Suppose I satisfies T and J satisfies S. What can be said about satisfying (S+T) ? It had better be the case that satisfaction is preserved under deletion!
Again, it seems clear that if we have two gofol texts then it ought to be possible to project back from a model of their sum to the gofol models of them. What exactly is the nature of this projection? It ought to be allowing the universe to shrink and tossing out some folds, is all. And of course any extensions that arent used go away automatically.
NOTE the new formulation using functions completely does away with the old problems about entailment and the deduction theorem. :-)
and that S entails T when every interpretation which satisfies S also satisfies T; that T is unsatisfiable when it has no satisfying interpretations; and that it is valid when it is satisfied by every interpretation of it.
All of these definitions are standard, but the fact that the folding maps required by SCL interpretations are in a sense selected by the text itself requires us to establish some lemmas which are trivial or unnecessary in most conventional accounts of first-order logic.
Lets rewrite this using 'atom/term' for 'holds/app'. KISS.
Consider any SCL kernel text no seqvars T written using names from some vocabulary V. One can translate this into a GOFOL text ha[T] with essentially the same meaning by applying the holds-app translation.
Might be best to do this without treating = specially, and distinguish these cases as ha= and rha=. Make this decision later when the lemmas are written.
The signature of ha[T] contains all of V, classified
as individual names, plus the countable sets {holds-0, holds-1,...}
of relation names with arities respectively 1, 2, ... and {app-0,
app-1,...} of function names with arities respectively 2, 3,...
, and the translation maps terms and atoms of T into those of ha[T]
by the recursive application of the following translation rules to every atomic
sentence in T
for any name n, ha[n] = n
for any term (t t1 ... tn), ha[(t t1 ... tn)] --> (app-n ha[t] ha[t1] ... ha[tn])
for any atom (t t1 ... tn) with t not equal to '=', ha[(t t1 ... tn)] --> (holds-n ha[t] ha[t1] ... ha[tn])
For example,
ha[(forall (x y) (implies (Boy x)) (exists (y)
(and (Girl y) (Kissed x y) (= y (lover x)) )))]
=
(forall (x y) (implies (holds-2 Boy x)) (exists (y) (and (holds-2 Girl
y) (holds-3 Kissed x y) (= y (app-2 lover x)) )))
The relation and function names of ha[T] play no real expressive role: they exist merely to provide a GOFOL 'wrapper', allowing every name in V to be treated uniformly as denoting non-relational entities in the universe, i.e. individuals in GOFOL.
Later we will show that T is satisfiable iff ha[T] is: in fact, that any model of T can be transformed into a model of ha[T], and vice versa. The construction is fairly obvious.
Its even nicer now, since the folds correspond exactly to the holds and apps.
If some symbols of V occur only in relation position in T, then a more restricted translation can be used in which the translation rules above are applied only to terms and atoms in V whose leading term has a subterm which also occurs in an object position, so that any parts of the vocbaulary which are strictly first-order are left unchanged by the translation. We will refer to this as rha[T]. For example, rha leaves the above example unchanged. This restricted translation is idempotent on GOFOL texts, unlike the full translation; but it has the severe practical limitation of not being preserved under textual combinations.
Write T;S for the text obtained by concatenating the texts T and S, then we have for any T and S,
ha[T] =/= T
and
ha[T;S] = ha[T] ; ha[S]
In contrast, for any GOFOL text T,
rha[T] = T
so that for example rha[rha[T]] = rha[T]; but there exist texts T and S with
rha[T;S] =/= rha[T] ; rha[S].
This will occur whenever a name is in object position in S but only in relation position in T, for example. An application which is translating SCL into GOFOL using rha could therefore find itself needing to re-apply the translation mapping when new sentences are added to a text, which is likely to be an unacceptable cost for many applications.
Part of the intended function of the SCL header is to allow an SCL module to 'declare' explicitly which of the symbols in its vocabulary do not occur in object position, enabling an SCL engine to safely translate SCL into GOFOL using the more efficient restricted rha mapping.
For convenience later, we define the inverse syntactic mappings ah and ahr by the equations ah[ha[x]] = x and ahr[rha[x]] = x
remark that seqvars can be translated using lists, which gets the whole language into GOFOL.
This whole section needs to be re-thought.
An SCL module is a named piece of SCL text, called the body
text, with an optional formal preamble called a header. A module
without a header is simply a named piece of SCL text which can be imported into
other text by using the name inside an scl:imports expression,
similar to an OWL ontology [refOWL].
Headers provide another level of functionality. The header is itself SCL text, interpreted using the same semantics (and hence subject to the same inference processes) as other SCL text; but the relationship between the semantics of the header and body text is special: in particular, the header is allowed to quantify over entities which are not in the intended universe of discourse of the body text. The primary intended roles of a header are to allow a module to describe its signature explicitly, to state syntactic conventions used in the body of the module, and to delineate and provide a name for the intended universe of discourse. These are often thought of as syntactic issues requiring translations between distinct languages: following the design principles of SCL, they are here handled withing the same language by using the same uniform semantic framework, allowing SCL processors to reason about the content of SCL modules. By convention, however, any inconsistency between the header of a module and the body text may be considered to be a syntactic error in the body text.
Headers may be defined to be countably infinite, provided that the effect of such an infinite header can be reproduced by a suitable computable operation on expressions. This convention can be used to provide a semantic connection between procedural 'attachments' or 'call-outs' and the model theoretic semantics, and to provide a coherent approach to the incorporation of data-structure conventions into SCL. This conventions, together with the use of the module naming convention, allows headers to describe certain kinds of 'closed-worlds', for example allowing SCL modules to act like databases when required.
-------------------
There are 2 issues here. One is simply the advantages of being able to check syntax and provide guarantees of mergability and of being in a particular subcase. The other is this whole business of comparing universes of discourse and merging requiring protective guards on quantifiers. We may need to abandon the latter for the first draft.
In order to describe the interpretation of headers we need a new semantic notion. Say that an interpretation I is a shrinking of J, and that J is an expansion of I, when I can be obtained from J by deleting some things from the universe of I and possibly some names from the vocabulary. Formally, when the vocabulary of I is a subset of that of J, intI(v) =intJ(v) and relJ(v)=relJ(v) for all v in the vocabulary of I; UI is a subset of UJ, RI is a subset of RJ, and for all x in RI, relJ(x) = relI(x). Intuitively, the expansion J may include new individuals and some entirely new relations, but it cannot change the extensions of relations named in I.
Then the semantics of a module with a header can be stated as follows: an interpretation I fits a module when it is an interpretation of the body and has an expansion which satisfies the header, and it satisfies the module when it fits the module and satisfies the body:
| if E is a | of the form | then I(E) = |
| module | (scl:head head ) body |
if I(body)=true and for some expansion J of
I, J(head)=true, then true; otherwise false |
Note that an interpretation which satisfies the body but which
cannot be expanded to satisfy the header is considered to be a non-fitting interpretation
of the module: this is the sense in which the conditions expressed by the header
are considered syntactic.The four relation names scl:Ind, scl:Rel,
scl:Fun and scl:Arity are called the header vocabulary.
The header vocabulary can be used anywhere in any SCL text; but when used in a module header, the semantic conditions require that the header classifications are understood to refer to interpretations of the body of the module, rather than of the header itself. To see the difference this makes, consider the following module with an empty header:
(scl:module example1 ( (not (scl:Ind R)) ))
This is a contradiction - has no satisfying interpretations
- since any interpretation which fits the inner sentence would require R
to denote an individual in U, but the sentence asserts that is not in U.
The sentence
(forall (x) (scl:Ind x))
is a tautology in any module body, since scl:Ind is true of everything
in the universe: one could in fact transcribe (scl:Ind term) in
the body (though not in the header) as any tautologous assertion, in particular
as ( term = term ).
However, the same sentence in the header yields a satisfiable module:
(scl:module example2 ((scl:head (not (scl:Ind R)) ) (R
a) ))
This is satisfied for example by an Herbrand interpretation
H in which the interpretation mapping is the identity, with UH={a},
RH={R} and extH(R)={<a>};
the fit is guaranteed by the extension J with UJ={a,
R}, RJ={R, scl:Ind} and extJ(scl:Ind)={<R>}.
Note that although R is an individual in J, it is not in H; and
that the interpretation rules for the entire module require that extH(scl:Ind)
= {<a>}.
If the body of the module had 'mis-used' the relation symbol as an individual name, for example:
((scl:head (not (scl:Ind R)) ) (Q R) )
then once again the module would be unsatisfiable, since there are no interpretations which fit such a module, so no interpretations which satisfy it. It is useful to distinguish this kind of unsatisfiability from an unsatisfiability arising from a simple contradiction in the body of the module, such as:
( (Q R) (not (Q R)) )
since in the former case the body alone is satisfiable. The contradiction in the first case arises from an essentially syntactic incompatibility between the fitting conditions proscribed by the header and the actual usage in the body.
We will describe this case, of a module which has no interpretations which fit it, as an unfit module. Unfit ontologies have no interpretations, so have no satisfying interpretations; but their unsatisfiability arises from a different source than a mere contradiction. SCL applications may consider an unfit module to be a syntactic error, even if the unfitness can only be detected by semantic reasoning processes.
The header vocabulary can be used in fairly obvious ways to
'declare' constraints on the allowable signature of a module. A conventional
first-order language can be specified by asserting scl:Ind of every
individual, scl:Rel of every relation, and scl:Fun
of every function, and specifying the arity of each relation and function using
scl:Arity. For example, the following header specifies a small
conventional first-order language signature suitable for expressing the earlier
example:
Need a different example
Im not entirely happy with this header vocabulary. It would be better to have the ontology name itself be used as the name of its universe. This would allow one module to refer to the universe of discourse of another universe, and allow 'bridging' ontlogies to declare relationships between alternative universes of discourse. The arity/relation/function stuff is really only needed for syntax checking, but the universe of discourse is something deeper.
Which leads to the following thought. We need to be able
to say that something is(/is not) in the universe of discourse, preferably in
a way which can also be used meaningfully in another ontology. Which suggests
a 'universe' functional, eg (scl:UOD ontologyname). The problem with this might
be that it uses non-GOFOL notation essentially: ((scl:UOD foo) x). Or we could
have a general convention that an ontology name used as a predicate is that
ontology's 'thing' classification... but this overloads the ontology name, which
the W3Cers won't like. OK, need to take a decision on this.
It smells like the datatype trick of using the name both as a class and as a
function. That overloading works OK, though, so why not this one?
BUt to return to the general point: what else do we need in the header vocabulary? To allow 'type checking' we need to be able to declare arity and functionality. Do we really need an explicit Rel?? Ans: yes, becus it has a direct syntactic check associated with it.
If Ind is relativized to an ontology, why aren't Rel and
Fun also relativized? Ans: because Ind alone is connected with the quantifiers
and with equality. In fact we need to get this connection with = sorted out
better. Maybe = is enough: (ind x) is just (= x x). Aha! We havnt said
what happens to the special vocabulary conditions in an expansion:
clearly this is of critical importance, need to get it right. This might be
the key.
Surely we will want = to mean = even in the header, right? So that meaning must
be extendable, which already is a problem with the definition of expansion given.
NEEDS MORE THOUGHT.
All of this is tightly connected with the SCL->GOFOL embedding and the need to treat = specially. There is one important thing hidden here which I havnt got it completely straight yet. The idea is that when talking about A from 'outside', one has to interpret its quantifiers as restricted to its universe. The header has to be explicit about this 'outside' view.
Another thought: should importing be sensitive to the UOD? That is, the simple OWL-inspired importing is based on this unrealistic notion of a shared UOD, maybe we need to do better since we are facing up to this issue. But the simple case must be available as a syntactic default, so how do we manage that? One guideline is that importing a plain module ought to be the default case: which suggests that it is the header itself which declares the universe of discourse; just plain SCL text has no such committment. In turn suggests analysing more carefully what that process of naming really amounts to. Importing M requires that (OUD M) is the universe of the quantifiers in the sentences of M. Importing text is just a committment to satisfy it. On this view, then, giving a name to a module is a bigger deal; but what has that got to do with the header?? Nothing, so we don't get the easy default. Hmmm.
The older intuition was that one could transfer the header into the body with some quantifier restrictions. If so, importing these ought to be similar.
(scl:head
(forall (x) (not (and (scl:Ind x) (scl:Rel x) )))
(scl:Rel Boy Girl Kissed)
(= 1 (scl:Arity Boy))
(= 1 (scl:Arity Girl))
(= 2 (scl:Arity Kissed))
)
The first sentence expresses the conventional that relation symbols must not be used as individual names and vice versa: this is satisfied by every conventional first-order signature. The arity assertions here take advantage of the SCL fitting conditions. Note that it is consistent to allow a relation to take several different numbers of arguments, in general, so for example this is consistent:
(scl:Arity 2 R) (scl:Arity 3 R) (scl:Arity 5 R)
but the use of 'scl:Arity' in a function position
requires that it denote a functional relation in any fitting interpretation;
so the only consistent way to interpret this header is with scl:Arity
interpreted as a functional relation, ensuring that all relations in the body
have a fixed number of arguments.
Note that if the body of a module is syntactically correct GOFOL, then including the appropriate header does not impose any extra conditions on the fit of an interpretation. It does however make these conditions explicit so that they can be checked.
Headers may also be used to declare special names of various forms. By convention, a header may be specified to be (equivalent to) a special name theory which consists of an recursively enumerable set of ground axioms specifying the positive and negative cases of some lexical categorization, typically the lexical space of a datatype represented by a predicate. Such headers can be imported into other headers, serving there as a form of declaration that the lexical forms are considered to be special names in the module body. In particular, SCL recognizes the built-in datatypes in XML Schema Part 2: Datatypes [XML-SCHEMA2], listed in the following table:
For each such name xsd:sss, the corresponding special
name header consists of the axioms
(xsd:sss (xsd:sss name))
for each name which is a legal lexical form for
xsd:sss;
(not (xsd:sss (xsd:sss name)))
for each name which is not a legal lexical form
for xsd:sss;
(= (xsd:sss name1) (xsd:sss name2))
for each pair of names which are legal lexical forms for xsd:sss
and map to the same item in the value space of xsd:sss.
The datatype name serves here both as a function (mapping the lexical form to
the value) and as a predicate on the value space: this follows the convention
used in RDF [refRDF]. In addition, we use the datatype URI reference as the
name for the module, so that the appropriate datatype can be included in a header
by writing for example:
(scl:import xsd:nonPositiveInteger)
in the header. Note that importing a special name theory into the body of a module amounts to including an infinite set of axioms, but importing it into a header only imposes the appropriate semantic conditions on the special names actually used in the the vocabulary of the body.
When the header of a module imports a special name theory, then all the legal lexical forms of the theory are considered to be special names in that module.
The two remaining constructions allow ontologies to be given global names and to be imported into other ontologies. The idea of naming a module makes sense only if we can assume some 'global' naming convention which has a larger scope than a single module, and which interpretations are required to respect. In XCL we will use URI references as global names. in accordance with the emerging WWWeb conventions, which are elaborately described elsewhere. For semantic purposes, we simply assume that there is a fixed function ont from module names to module values. The exact nature of module values is not specified, other than that they are entities which can be parsed into SCL kernel syntax and to which an interpretation mapping can be applied. (One can think of a module value as a quoted string containing a character representation of a module written using the kernel syntax.)
| if E is an | of the form | then I(E) = |
| phrase | (scl:import name) |
false if I(ont(name)) = false, otherwise true |
| module definition | (scl:module name = (text)) |
if for any interpretation J, J(ont(name))
= true iff J(text) = true, then true; otherwise false. |
An assertion of a module definition is required to have miraculous semantic powers: if it is ever true in any interpretation, then the name is attached to the defined module in all interpretations. Thus, if by convention we say that publishing any SCL module definitions amounts to asserting it, then a publication of a module definition requires any interpretation of any SCL module containing an importation of that name to treat it as having the same effect as copying out the sentences of the defined module in place of the importation. To actually achieve such miraculous powers requires a global naming convention: XCL uses universal resource identifiers [refRFC2396] for this purpose.