LAST POSTED Feb 3, 2004
Feb 9 2004. This version is obsolete. For a more recent version check here.
SCL is a first-order logical language intended for information exchange and transmission. SCL allows for a variety of different syntactic forms, called dialects, all expressible within a common XML-based syntax and all sharing a single semantics.
<history: KIF, CL, unification, reducing complexity; needs of the SW.>
Most of the design aspects of SCL can be understood as arising from the following scenario.
Two people, or more generally two agents, A and B, have each used conventional first-order logic to formalize some knowledge. They now wish to communicate this knowledge to a third agent C which will make use of the combined information so as to draw some conclusions. The goal of SCL is to provide a logical framework which can support this kind of communication and use without requiring complex negotations between the agents. This ought to be simple, but in practice thre are many barriers to such communication.
First, A and B may have used different surface syntactic forms to express their knowledge. This is a well-known problem and various proposals have been made to solve it, usually by defining a standard syntax into which others can be translated, such as KIF [refKIF]. SCL tackles this issue similarly by providing a common syntactic framework into which many superficially different syntactic forms can be mapped, and an XML-based common framework for transmitting the basic logical structure in a variety of surface forms.
Second, A and B may have made divergent assumptions about the logical signatures of their formalizations. For example, a particular concept, such as marriage, might be represented by A as an individual, but by B as a relation. Often, one can give mappings between the logical forms of such divergent choices, many of which are widely familiar; but in a conventional FO framework, these have to be considered meta-mappings which translate between distinct formalizations; and very few general frameworks exist to define such meta-syntactic mappings on a principled basis or in a form suitable for use by software agents. This problem has not been so widely recognized or discussed as the first, but it is ubiquitous. SCL tackles this issue by as far as possible removing the conventional limitations on first-order signatures, allowing apparently divergent styles of formalization to co-exist and the relationships between them to be expressed axiomatically when required. For example, a name in SCL may serve both as an individual name and as a relation name. Much of the semantic development described in this document is concerned with this issue.
Third, A and B may have been writing with different intended universes of discourse in mind. This kind of situation is quite common: very few ontology composers are able to bear in mind that their assertions might be understood to be talking about things that they have not even conceived of. The results, when formal axioms are combined naively, can be quite unpredictable. If one is thinking about taxonomic classifications of animals, say, it is often difficult to bear in mind that the complement of the set of mammals may be taken to include fruit, sodium molecules, styles of avant-garde paintings or the names of fictional characters in movies. SCL provides a special 'top-level' syntactic form called a module which automatically gives a name to the universe of discourse of a named ontology, and automatically inserts guards on any contained quantifiers when information is combined. This form is optional, to allow for applications where logical sentences are intended to be combined without applying any such transformations; but its use has many incidental advantages for general information exchange on a network, among them being that all such information is automatically expressed in a decideable subcase of FO logic.
SCL also has some other features intended to facilitate information exchange, including a general technique for using information from externally defined datatypes and databases.
Historically, the SCL project arose from an effort, called the Common Logic initiative, to update and rationalize the design of KIF [refCL][refKIF], which was first proposed as a 'knowledge interchange format' over a decade ago and, in a simplified form, has become a de facto standard notation in many applications of logic. Several features of SCL, most notably its use of sequence variables, are explicitly borrowed from KIF. However, the design philosophy of SCL differs from that of KIF in various ways, which we briefly review here.
First, the goals of the languages are different. KIF was intended to be a common notation into which a variety of other languages could be translated without loss of meaning. SCL is intended to be used for information interchange over a network, as far as possible without requiring any translation to be done; and when it must be done, SCL provides a single common semantic framework, rather than a syntactically defined interlingua.
Second, largely as a consequence of this, KIF was seen as a 'full' language, containing representative syntax for a wide variety of forms of expressions, including for example quantifier sorting, various definition formats and with a fully expressive meta-language. The goal was to provide a single language into which a wide variety of other languages could be directly mapped. SCL, in contrast, has been deliberately kept 'minimal': the kernel in particular is a tiny language. This makes it easier to state a precise semantics and to place exact bounds on the expressiveness of subsets of the language, and allows extended languages to be defined as encodings of axiomatic theories expressed in SCL, or by reduction to the SCL kernel.
Third, KIF was based explicitly on LISP. KIF syntax was defined to be LISP S-expressions; and LISP-based ideas were incorporated into the semantics of KIF, for example in the way that the semantics of sequence variables were defined. Although the SCL core surface syntax retains a superficially LISP-like appearance in its use of a nested unlabelled parentheses, and could be readily parsed as LISP S-expressions, SCL is not LISP-based and makes no basic assumptions of any LISP structures. The recommended SCL interchange notation is based on XML, a standard which was not available when KIF was originally designed.
Finally, many of the 'new' features of SCL have been motivated directly by the ideas arising from new work on languages for the semantic web [refSW], and in particular, SCL is intended to be useable as a slightly improved Lbase [refLbase], i.e. as serving the role of a semantic reference language for other SW notations.
It is clear that the 'same' logical expression can be rendered in a variety of different syntactic, or even graphical, forms: connectives can be written as infix, postfix or prefix, groupings indicated by brackets, groups of dots or graphically by enclosing circles, etc.. The differences in appearance between surface forms can be quite extreme. A simple logical expression written in introductory text-book form:
(∀x)(Boy(x) → (∃y)(Girl(y) & Kissed(x,y)))
appears in conceptual graph interchange form (CGIF) as:
[@every *x] [If: (Boy ?x) [Then: [*y] (Girl ?y) (Kissed ?x ?y) ]]
which is itself a 'linear' rendering of a diagrammatic representation:
@@ insert diagram as figure
The same expression in a KIF-like syntax is:
(forall (?x ?y) (implies (Boy ?x)) (exists (?y) (and (Girl ?y) (Kissed ?x ?y))))
Extremely compact notations have been used, such as the postfix convention which requires no parentheses:
KissedxyGirly&EyBoyxIAx
while at the other extreme, a hypothetical XML notational style might look like
<formula>
<forall>
<var>x</var>
<formula>
<implies>
<formula>
<atom>
<con>Boy</con>
<var>x</var>
</atom>
</formula>
<formula>
<exists>
<var>y</var>
<formula>
<and>
<formula>
<atom>
<con>Girl</con>
<var>x</var>
</atom>
</formula>
<formula>
<atom>
<con>Kissed</con>
<var>x</var>
<var>y</var>
</atom>
</formula>
</and>
</formula>
</exists>
</formula>
</implies>
</forall>
</formula>
To provide for information exchange between such a plethora of syntactic alternatives,
SCL follows the lead of the KIF initiative by providing a single 'standard'
logical language, called the SCL core (with a syntax based largely
on KIF), and a general technique for translating other notations, called SCL
dialects, into the core syntax. In fact, a subset of the
SCL can however be expressed a variety of dialects, and this document defines several which provide SCL variants similar to existing logical notations in widespread use, and a general XML-based syntax, XCL, for general purposes of information exchange. XCL allows assertions to declare their dialect, and so can be used as a general-purpose interchange notation and mark-up language for any conforming SCL syntax. Finally, a general technique for defining SCL dialects in terms of an SCL abstract syntax is described. XCL is considered to be the definitive 'abstract syntax' of SCL, in the sense that any language whcih can be parsed into XCL so as to preserve its semantic meaning can be considered to be an SCL dialect.
In addition to providing for many divergent surface syntactic forms, SCL is designed to allow expressions to be used without making explicit lexical assumptions. Conventionally, a first-order language is defined relative to a particular signature, which is a lexicon sorted into disjoint sublexica of individual names, relation names and perhaps function names, the latter two each associated with a particular arity, i.e. a number of arguments with which it must be provided. This provides a simple context-free method of checking that all terms and atomic sentences will be well-formed, and ensures that any expression obtained by substitution of well-formed terms for variables will be assigned a meaningful interpretation.
The notion of signature is appropriate for textbook uses of logic. Applied to an interchange situation, however, where sentences are distributed and transmitted over a network (in particular, on the WWWeb) and may be utilized in ways that are remote from their source, this would require that a single global convention for signatures be adopted, which is impractical. SCL therefore is designed to have no built-in assumptions about signatures: it allows information to be combined even when it is written using divergent assumptions about the appropriate signature. This has a number of consequences.
First, SCL must be able to accomodate expressions in which a term is used both as an individual name and as a relation name, or cases where a relation name is used with different numbers of arguments, or as both a relation and a function name. To this end, SCL is defined with a very accomodating syntax which places minimal restrictions on the lexical roles of names or indeed of terms more generally, and allows relationships between alternatives to be expressed in the language itself.
Such cases arise often in practice. For example, the idea of marriage can be rendered in a formal ontology as a binary relation between persons, or a more complex relation between persons, legal or ecclesiastical authorities and times; or as as a legal state which 'obtains', or as a class or category of 'eventualities', or as a kind of event. Much the same factual information can be expressed with any of these ontological options, but resulting in highly divergent signatures in the resulting formal sentences. Rather than requiring that one of these be considered to be correct and the others translated into it by some external syntactic transformation, SCL allows them all to co-exist, often allowing the connections between the various ontological frameworks to be expressed in the logic itself. For example, consider the following sentences (all written in the SCL core syntax):
(married Jack Jill)
(married (roleset: (husband Jack) (wife Jill))
(exists (x)(and (married x) (husband Jack x) (wife Jill x)))
(= (when (married Jack Jill)) (hour 3 (pm (thursday (week 12 (year 1997)))))
)
(= (wife (married 32456)) Jill)
(ConjugalStatus married Jack)
((ConjugalStatus Jack) Jill)
These all express similar propositions about a Jack and Jill's being married,
but in widely different ways. The logical name married appears
here as a binary relation between people; a unary property of a state of affairs,
with associated roles and fillers; a three-place relation between two persons
and a time; a function from numbers to individuals; as an individual 'status',
and finally, although not named explicitly, as the value of a function from
persons to predicates on persons. In SCL all these forms can be used at the
same time: the conjunction of the above set of sentences is syntactically correct
SCL, which does not impose any restriction on the occurrence of terms in
other atoms or terms: any term may occur in any position in any atomic
sentence or term. This lexical freedom requires that SCL allow quantification
over relations and functions, for example, and the use of relation-valued functions,
and relations applied to other relations. The resulting syntax is similar to
a higher-order syntax; but unlike traditional omega-order logic, SCL syntax
is completely type-free. It requires no allocation of higher types
to functionals such as ConjugalStatus, and imposes no type discipline.
For example, self-application is syntactically legal in SCL, as in:
(is-Relation is-Relation)
Readers familiar with conventional first-order syntax will recognize that this syntactic freedom is unusual, and may suspect that SCL is a higher-order logic in disguise. However, as has been previously noted on several occasions [ref HILOG][refHenkin?], a superficially 'higher-order' syntax can be given a completely first-order semantics, and SCL indeed has a purely first-order semantics, and satisfies all the usual semantic criteria for a first-order language, such as compactness and the Skolem-Lowenheim property.
What makes a language semantically first-order is the way that its names and quantifiers are interpreted. A first-order interpretation has a single homogenous universe of individuals over which all quantifers range; any expression that can be substituted for a quantified variable is required to denote something in this universe. The only logical requirement on the universe is that is a non-empty set. Relations hold between finite sequences of individuals, and all that can be said about an individual is the relations it takes part in: there is no other structure. Individuals are 'logically atomic' in a first-order language: they have no logically relevant structure other than the relationships in which they participate. Expressed mathematically, a first-order intepretation is a purely relational structure. It is exactly this essential simplicity which gives first-order logic much of its power: it achieves great generality by refusing to countenance any restrictions on what kinds of 'thing' it talks about; it requires only that they stand in relationships to one another.
Contrast this with for example higher-order type theory, which requires an interpretation to be sorted into an infinite heirarchy of types, satisfying very strong conditions. In HOL, a quantification over a higher type is required to be understood as ranging over all possible entities of that type; often an infinite set. The goal of higher-order logic is to express logical truths about the domain of all relations over some basic universe, so a higher-order logic supports the use of comprehension principles which guarantee that relations exist. In contrast, SCL only allows the universe to contain relations, but imposes no conditions on what relations exist other than those required to ensure that every name has a referent.
In FO semantics, a relation name is interpreted as denoting a set of sequences of individuals, being the sequences between which the relation holds: call this a relation set, or a relational extension. In the SCL syntax, the same name might be used to refer to an individual. To retain the essentially first-order nature of the interpretation in cases like this, SCL assumes that a relation name used as an individual name must refer to an individual which, if it is ever called upon the play the role of a relation, is true of exactly the same sequences. The relational individual is 'associated' with same relation set as its name. This ensures that the name retains a single meaning in all contexts of use. In stating the formal semantics we will call this association mapping rel, so that if <name> is intepreted both as a relation, using the mapping R, and as an individual, using I, then R(<name>)=rel(I(<name>))
Note that we do not assume that the individual denoted by the relation symbol is the relation set itself. While that interpretation might be thought set-theoretically more natural, to require an individual to be a large set containing structures containing other individuals would be a clear violation of the essentially first-order nature of SCL semantics.
This semantic strategy also allows several distinct individuals to be associated with the same relational extension, which provides an extra measure of descriptive flexibility. One can think of a relational individual as a relation in an intensional sense, and a relation set as a relation in a narrower extensional sense. SCL may be said to embody an intensional theory of relations as objects, although the SCL truth-conditions are purely extensional.
Finite sequences play a central role in SCL syntax and semantics. All atomic sentences consist of an application of one term, denoting a relation, to a finite sequence of other terms. Such argument sequences may be empty, but they must be present in the syntax, as an application of a relation term to an empty sequence does not have the same meaning as the relation term alone.
SCL also allows relations to be take any number of arguments: such a relation
is called variadic. (Married is an example of a variadic
relation.) SCL follows KIF also in providing a special syntactic form called
sequence variables to allow generic assertions to be made which apply
to arbitrary argument sequences. An SCL axiom using sequence variables can be
viewed as a first-order axiom scheme, standing in for a countably infinite set
of first-order instances.
If an argument sequence ends with a sequence variable, then the presence of the variable indicates that the sequence may be arbitrarily extended, and the sentence is required to hold for all the possible extensions.
Sequence variables are quite a powerful device: in effect, they allow a finite sentence to assert infinitely many quantifications all at the same time. Indeed, if arbitrary quantification over sequence variables is permitted, then the resulting language is a subset of the infinitary logic Lw1w, of a higher expressiveness than first-order logic, and for example is not compact [refHayMenzel]. The restrictions on sequence variables in SCL have been chosen to restrict the language to first-order while providing much of the practical utility of sequence variables for writing 'recursive' axioms to define lists and other recursively defined constructions.
Sequence variables are restricted in SCL to occur only in the last position in an argument sequence, and are not bound by quantifiers: this keeps the language first-order and makes unification decideable [refKutsia]. Sequence variables can be replaced by a more conventional notation, at some considerable cost in elegance, by introducing argument lists explicitly: we provide a generic header which can be used for this kind of elimination, which is commonly adopted in practical KR notations.
SCL treats functions, semantically, as a special class of relations. A relation
is functional at n, or n-functional, when
it holds of a single, unique first argument for each sequence (of length n)
of the remaining arguments; and it is functional above n when it is
m-functional for every m greater or equal to n; and simply functional
when it is functional above 0. The SCL convention is that the first argument
is the value of the relation applied to the remaining arguments; thus, if R
is a relation symbol denoting a 2-functional relation then the equation
a = R(b c) is is similar in meaning to the atomic sentence R(a
b c).
This differs from the convention used in Prolog [refProlog]
where the function value is written as the last argument of a relation.
The present convention was chosen to better integrate with the use of sequence
variables. Note that the arity of the function is the number of relational
arguments, so is one more than the number of functional arguments: in this case
the arity of R is 3.
Assimilating functions to relations in this way is straightforward, and indeed is standard practice; but the presence of function symbols in a piece of SCL syntax greatly complicates the statement of the model theory. This is because function symbols can be used, in effect, to create new names, by substituting terms as arguments in other terms. The simple presence of a function symbol therefore provides an infinite set of names, conventionally called the Herbrand universe; and any first-order semantics must be stated in such a way that every such term has a well-defined denotation. In a conventional logical framework this is guaranteed by the signature, since every function symbol is assigned a fixed number of arguments and is required to denote a function of the appropriate arity; but for SCL a more subtle criterion is required, called fitting. An interpretation of a set of SCL sentences is required to fit those sentences, in a sense made precise below but which can be intuitively characterized as being required to provide a well-defined interpretation for every term in the Herbrand universe, i.e. every term that can be obtained by substitution of terms for variables, i.e. every possible expression which refers to an individual. The presence of variables in function terms and the use of sequence variables both impose quite strong conditions, in some cases amounting to the requirement that everything in the universe have a corresponding relational extension which is functional. However, it is easy to show that any interpretation can be trivially extended to one which satisfies the requirements.
SCL text is any set or sequence of SCL top-level sentences, called SCL phrases; an SCL module, or simply a module, is some SCL text together with an optional header, which is itself SCL text.
The SCL core syntax uses sequences throughout, for convenience in defining iterative syntactic operations, but no particular significance attaches to the ordering of the sequence, and other SCL dialects may adopt a set-based syntactic convention.
The terminology of "text" and "module" is intended to be a neutral terminology used to refer to any coherent piece of SCL which can be published, transmitted or asserted as a single document. It is not intended to convey any particular categorization or to indicate an intended use or philosophical stance. Other terms in widespread use in various communities include "ontology", "knowledge base", "axiom set" , "set of sentences", "metadata", "data model" and "model", as well as such particular usages as "RDF graph" and "document".
Headers have a special semantic role and are treated in a distinct way in the semantics: they provide a general method for encoding syntactic and other 'background' information about the module. A special header vocabulary is provided which is sufficient to describe many standard signatures and syntactic conventions; but any SCL text may be included or imported into a header.
The core also provides a top-level module definition syntax which associates a name with a module, and a importing syntax, which indicates that a named module is being included into another module. The intended meanings of these constructions are fairly obvious, but the formal semantic statement requires that we assume the existence of a global module-naming convention, and that module names refer to entities in formal interpretations. This can all be stated abstractly, but is more directly conveyed by the observation that SCL uses the emerging semantic web conventions, as used in RDF and OWL, which are based on the W3C URI naming protocols [ref RFC2396]. This "top-level" SCL syntax also provides for modules to declare their intended domain of discourse, and other functions intended to be useful in exchanging information.
The SCL Core is the basic syntactic form of SCL relative to which the semantics is defined, and which is used to give examples throughout this document. It is not the recommended SCL syntax for information exchange. The choice of syntax for the core is somewhat arbitrary, but was based on KIF for historical legacy reasons and because this form, although slightly unconventional in appearance to an eye accustomed to textbook logical forms, has several advantages for machine processing. The SCL core syntax is not exactly that of KIF 3.0 [refKIF], and it defines a considerably smaller language.
Apart from being a smaller language, SCL Core syntax differs
from KIF in the following respects.
(1) Variables are not required to be marked syntactically, and free variables
are impossible.
(2) The double-quote symbol " is prohibited in SCL Core. This permits quoted
SCL Core syntax to be included inside XHTML markup without being rendered by
a Web browser. Otherwise, SCL Core syntax permits the use of the full Unicode
character set.
(3) .... finish this list later
Any SCL Core, or core, expression is encoded as a sequence of Unicode characters ( UCS-2, from the Unicode 'base multilingual plane' according to ISO/IEC 10646-1:1999). The standard encoding is UTF-8 (ISO 10646-1:2000 Annex D ) . Only characters in the US-ASCII subset are reserved for special use in the core itself, so that the language can be encoded as an ASCII text string if required. UCS-2 characters outside that range are represented in ASCII text by a character coding sequence of the form \unnnn or \unnnnnn where n is a hexadecimal digit character. When transforming an ASCII text string to UTF-8, such a sequence should be replaced by the corresponding UTF-8 byte encoding. This document uses the ASCII encoding.
Some of these unicode references are buggy and need checking.
The syntax of the core is designed to be easy to process mechanically. The syntax is defined in terms of disjoint blocks of characters called lexical items or lexemes . A character stream can be converted into a stream of lexemes by a simple process of lexicalisation which checks for a small number of interlexical characters, which indicate the end of a lexical item (and sometimes the start of the next one.) The interlexical characters are: single quote ' (U+0060), open and closing parenthesis ( U+0028 and U+0029) and any whitespace character: in ASCII, these are space (U+0020), tab (U+0009) line (U+000A) page (U+000C ) and return (U+000D) The backslash character \ (reverse solidus U+005C) also plays a role in lexicalization, by cancelling the interlexicality of the immediately following character. Certain characters are reserved for special use as the first character in a lexical item, and the characters less-than < (U+003C), greater-than > (U+003C) and double-quote " (U+0022) are forbidden, and should be replaced by a suitable encoding, which may be the Unicode character coding sequence described above, or another character encoding mandated by the conventions used in any surrounding or enclosing document.
The backslash \ (reverse solidus U+005C) character is reserved for special use. Backslash \ plays a special role in enabling "out of code" characters to be included in core text. Followed by the lowercase letter u (U+0075) and a four- or six-digit hexadecimal code, it is used to transcribe non-ASCII UTF-8 characters, as explained above. Any string of this form plays the same syntactic role in an ASCII string rendering as a single ordinary character. Backslash is also used as a cancelling prefix. The special roles of any of the interlexical or marking characters, and of the backslash character itself, can be cancelled by preceding the character with a backslash. This enables marking and interlexical characters to be included in lexical items without writing their Unicode equivalents, and permits hexadecimal Unicode codes to be transmitted as ASCII character strings in contexts which would otherwise require Unicode conversion.
The following syntax is written using EBNF: | indicates alternatives, * indicates any sequence of expressions, + indicates any nonempty sequence, - indicates an exception, and parentheses are used as grouping characters. The EBNF also applies to UTF-8 encodings, with the change noted to the category nonascii.
1. Character classification
S ::= (space|tab|line|page|return)+
lexbreak ::= S | '(' | ')'
alpha ::= 'A' |...| 'Z' | 'a' |...| 'z'
digit ::= '0' |...| '9'
special ::= '@' | ''' | '"' | '<' | '&'
other ::= any other ASCII non-control character
2. Lexical analysis
hexa ::= digit | 'A' |...| 'F' | 'a' |...| 'f'
nonascii ::= '\u' hexa hexa hexa hexa | '\u' hexa hexa hexa hexa hexa hexa
Note. For UTF-8 strings, nonascii should be understood
to be the set of all non-control characters of UTF-8 outside the ASCII range,
ie all non-control characters in the range U+007F to U+FFFFFD. The use of the
\uXXXX sequence in UTF-8 character strings, while not illegal, is deprecated.
Note, the less-than character '<', the ampersand '&', and the double-quote
character '"' should not appear anywhere in any SCL core text; these exclusions
allow SCL core text to be safely included in XML documents.
seqvarchar ::= alpha | digit | other | nonascii
namechar ::= alpha | digit | other | nonascii | '@'
stringchar ::= namechar | lexbreak | '\''
Note. Quoted strings are the only SCL lexical items that can
contain whitespace. A quoted string can contain any SCL character except double
quote, less-than or ampersand. A single-quote character can occur inside a quoted
string only when immediately preceded by a backslash character. \' indicates
the presence of a quote mark in the string, \\' indicates the presence of a
double quote mark in the string, and \\ followed by any other character than
single quote, or \ followed by any other character than ' or \ or u, indicates
the presence of a single backslash character in the string; \u may be the initial
part of a nonascii sequence which indicates the Unicode character
in the string, but if it is not part of such a sequence then it simply indicates
itself. These conventions are understood as applying in left-to-right order.
With these conventions, a quoted string indicates the string enclosed in the
quote marks. For example, the quoted string 'a\b\'c' indicates the string a\b'c,
and 'a\b \\\\'\'c\'' indicates the string: a\b \"'c'.
3. Lexical syntax
numeral ::= digit+
quotedstring ::= ''' stringchar* '''
reservedElement ::= 'and' | 'or' | 'iff' | 'implies' | 'forall' | 'exists' |
'not' | 'roleset:' | 'scl:imports' | 'scl:header' | 'scl:module'
Note change: 'reserved' distinct from 'special'. Also equality is NOT reserved.
Also, 'roleset: is needed to disambiguate the role syntax. Also, scl:imports
and scl:header are not special names but reserved syntax forms.
name ::= specialname | ( ( alpha | other ) wordchar* ) - reservedElement
specialname ::= '=' | 'scl:arity' | 'scl:Ind' | 'scl:Rel' | 'scl:Fun' | 'scl:Integer'
| 'scl:String' | numeral | quotedstring Note equality
is now a specialname. And scl:imports and scl:header are not names, cf above.
And Fun is needed.
seqvar ::= '@' wordchar+
Note. ReservedElement consists of the strings which should not be used as names in the SCL core syntax, since they are used to indicate the syntactic structure itself. Specialname is a category of names to which SCL attaches particular semantic meanings. Other SCL dialects may extend this category to include other name forms reserved for special use, and headers may declare other classes of special names. If a special name is used in any SCL text then its meaning as a special name cannot be over-ridden by any other interpretation of that text, so inappropriate uses of special names may produce inconsistencies.
4. Core expression syntax
Note. All core expressions consist of a pair of parentheses
enclosing the logical subexpressions of the expression in question, usually
with a word immediately following the opening parenthesis which indicates the
logical category of the expression. Atoms and terms are written in the form
(R a b) rather than the more usual R(a b) in a 'textbook'
syntax. The role of whitespace and parentheses in the syntax can be summarized
by the observation that whitespace is always optional except to separate names
in a term sequence, and that syntactic divisions between expressions are mostly
indicated by the occurrence of parentheses.
The atomic sentence syntax allows for an optional 'role-value' notation for
assigning arguments, and both terms and atoms allow arbitrary terms to occur
in the relation or function position. Quantifiers may restrict variables to
a named category. A@@@
termseq ::= (term S?)* seqvar?
term ::= name | '(' S? term S termseq S? ')' | '('quotedstring S term S? ')'
Note change: name includes specialname
Note, equation is ordinary atom so not broken out
as syntactic case
atom ::= '(' S? term S termseq S? ')' | '(' S? term S? '(roleset:' rolepair*
S? '))'
rolepair::= '(' S? name S term S? ')' Note,
space is obligatory after the name, and the equality sign has been omitted
boolsent ::= '(' (( 'and' | 'or' ) S) (sentence S?)* ')' | '(' ( 'implies' |
'iff' ) S? sentence S? sentence S? ')' | '(not' S? sentence S?')'
quantsent ::= '(' S? ( 'forall' | 'exists' S? ) '(' S? ( name | '(' S? name
S term note, term not name S? ')' S? )* ')'
S? sentence S? ')'
sentence ::= atom | boolsent | quantsent | '('quotedstring S? sentence ')'
sclphrase ::= '(scl:imports' S name S? ')' | sentence | '(' quotedstring ')'
note, name changed from 'topsentence'
scltext ::= ( sclphrase S?)*
moduledefinition ::= '(scl:module' S? name S? '(' ( '(scl:header' scltext ')'
)? S? scltext '))'
Apart from the top-level syntax for defining headers and ontologies, the only unconventional aspects of SCL are the syntax for atomic sentences and terms, which reflect the type-free catholicity imposed by the need to allow multiple lexical perspectives to co-exist. This section discusses these features in more detail.
A sequence variable stands for an 'arbitrary' sequence of arguments. Since
sequence variables are implicitly universally quantified, any top-level expression
in which a sequence variable occurs has the same semantic import as the countably
infinite conjunction of all the expressions obtained by replacing the sequence
variable by a finite sequence of variables, all universally quantified at the
top level. For example, the top-level sentence (R @x) has the same
meaning as the infinite conjunction:
(and
(R)
(forall (x)(R x))
(forall (x y)(R x y) )
(forall (x y z)(R x y z))
... )
This includes the empty-sequence case with no arguments. To
avoid this, use a variable followed by a sequence variable: (R x @y).
Sequence variables can be used to write 'recursive' axiom schemes. Rather than attempt a fully general description of this technique, we will illustrate it with a canonical example. Consider the following sentences:
(= nil (list))
(forall(x z)(iff (= x (list @y) (= (cons z x) (list z @y)))
which have the same meaning as the infinite set of sentences:
(= nil (list))
(forall (x z x1) (iff (= x (list x1)) (= (cons z x) (list z x1)) ))
(forall (x z x1 x2) (iff (= x (list x1 x2)) (= (cons z x) (list z x1 x2)) ))
(forall (x z x1 x2 x3) (iff (= x (list x1 x2 x3)) (= (cons z x) (list z x1 x2
x3)) ))
...
(forall (x z x1 x2 ... xn) (iff (= x (list x1 ... xn) (= (cons z x) (list z
x1 ... xn)) ))
... )
which clearly entails for any finite sequence t1... tn of terms,
that
(= (cons t1 (cons t2 (cons ...(cons tn nil)...))) (list t1 ... tn) )
and thus provides the familiar technique of writing a sequence of items as a cons-nil list, first used in LISP and more recently as the RDF 'collection' vocabulary [refRDF]. The tail-recursion represented by the axiom is re-expressed here as induction on the length of a proof.
SCL sequence variables do not actually provide a true recursive definition, as the 'schema' can be used only as a source of assertions and cannot itself be derived by using an inductive argument. The more powerful language obtained by allowing sequence variables to be bound by sequence quantifiers does provide true recursive powers, and is therefore in a higher expressive class than any first-order language. It is, for example, not compact. A more tractable language can probably be obtained by adding an explicit 'least fixed point' operator, but this idea goes beyond the scope of this document.
This general technique of imitating tail-recursive definitions by writing them as implications using sequence variables was pioneered by KIF [refKIF] and is one of the primary uses for sequence variables in SCL. What this construction shows, however, is that the use of sequence variables can be replaced, when required, by the use of explicit cons-nil lists as arguments, represented in SCL by nested terms. This convention is widely used in logic programming applications, and in RDF and OWL. The general rule can itself be stated in SCL by using seqvars:
(forall (x) (iff (x @y) (x (list @y)) ))
This thus provides a general technique for replacing the use of sequence variables by explicit quantification over argument lists. The costs of this translation are a considerable reduction in syntactic clarity and readability, and the need to allow lists as entities in the universe of discourse; the advantage is the ability of rendering arbitrary argument seqences using only a small number of primitives with a fixed, low arity. SCL can use either convention or both together, and can describe the relationship between them.
Atomic sentences which use the roleset: construction, for example
(Married (roleset: (wife Jill) (husband Jack)))
are considered to take a set of arguments in the form of role-value pairs. In this role-set syntax, the connection between the relation and its arguments is indicated by the role labels rather than by position in an argument sequence, which avoids the necessity of remembering the argument order when writing sentences, and provides some insurance against errors arising from sentences using different argument-order conventions.
In SCL, the roles are considered to be binary relations between an entity to which the main predicate applies and the argument, so for example the above atom is equivalent to the existential conjunction:
(exists (x) (and (Married x) (= Jack (husband x)) (= Jill (wife x)) ))
where x indicates an entity which has been variously called an
eventuality, fact, situation, event, state or trope,
and might be rendered in English as "Jack and Jill's being married"
or "the marriage of Jack and Jill". For SCL purposes however it is
possible to think of x more prosaically as being an argument sequence,
and the role-names as selectors on the elements of this sequence.
This syntax allows arguments to be provided in a piecemeal
fashion, and allows arguments to be omitted: such arguments are implicitly existentially
quantified. In fact, any such atom entails a similar atom with some role-pairs
omitted. Notice the difference in meaning between R, (R)
and (R (roleset:)). The first is a term which denotes the
realtional entity; the second is an atomic sentence which asserts positively
that R is true of the empty sequence; while the third, also an
atomic sentence, merely asserts that R is true of something, to
which other things may be related by unknown roles; for example, (Married
(roleset:)) asserts simply that a marriage exists.
This role-set convention does not itself specify any relationship between the same fact expressed as a role set and by using an argument sequence: but since SCL allows variadic relations, it is possible to use the same relation in both ways, and they can be related axiomatically. For example,
(forall (x y) (iff (Married x y) (exists (z) (and (Married
z) (= x (wife z)) (= y (husband z))) ))
indicates the convention by which a wife must be the first argument of a marriage. Again, SCL provides for both kinds of syntax, separately or together, and can describe a relationship between them using SCL axioms.
Any term which occurs as the first term in any atomic sentence or term is said to occur in relation position; any term t which occurs as the first term in any other term of the form (t t1 ... tn) is said to occur in function position on n; if it is the first term in another term of the form (t t1 ... tn @x) with a sequence variable then it said to occur in function position above n, or equivalently to occur in function position on m for all m>n; and finally, any name occurring as an argument of any other term or atom, and any application term, is said to occur in object position. These generalize the usual notions of signature category for relation, function and individual names. If T is a piece of SCL text then a term occurs in T in some position just when it occurs in that position in any atom or term occurring as a subexpression anywhere in T. A single term may occur in more than one position.
Note that anything in a function position is also in relation position, reflecting the SCL convention that functions are a category of relation.
For example, in the following text (which is not intended to be particularly meaningful):
(iff (forall (x) (= (f (f x)) (f x)) )) (idempotent f)) ((f joe) joe
@y)
the terms f, x, joe, (f x),
(f joe) and (f (f x)) all occur in object position; the
terms idempotent, =, (f joe) and f
all occur in relation position; and among the latter, f occurs
in function position on 1 while (f joe) occurs in function position
above 1.
The semantic significance of this is that any application term, and any name in object position, is required to denote something in the universe of discourse; while any term standing in a relation position is required to play the role of a relation, i.e. to have an associated relational extension, which must be appropriately functional when the term is in a fucntional position. When a single term occurs in both object and relation position, the entity in the universe which it is required to denote is itself required to play the relational role. Since quantified variables are required to range over the universe, any variable occurring in relation position requires that everything in the universe have an associated relational extension so that it can play a relational role; and if the variable occurs in a function position then these relational extensions are required to be appropriately functional. Overall, we refer to these requirements as the interpretation fitting the text. Interpretations which do not fit a text may be unable to determine a truthvalue for all instances of expressions in the text.
Several special cases of the kernel syntax can be identified, largely by restrictions on the syntax of atomic sentences and terms.
Text is @@@
Text is first-order if it contains no sequence variables, the only terms which occur in relation or function positions are names, and every name occurs in only one kind of position. If no term occurs in function or relation position in two atoms or terms with different numbers of arguments, then the text is fixed-arity. Fixed-arity first-order text corresponds to the traditional notion of a first-order signature: the names in the vocabulary can be subdivided into relation, function and individual names, each occurring only in its alloted role in the syntax, and with each function or relation having a fixed arity. Thus, fixed-arity first-order text can be considered to be conventional first-order syntax; we will refer to this case as GOFOL.
If no variable occurs in any term in function position, then the text is rigid. Rigid modules represent a useful compromise between the syntactic freedom of general SCL and the syntactic predictability of a conventional first-order syntax, as the fitting conditions on an interpretation are much easier to state and to check when quantifiers cannot bind function names. Notice that rigidity only restricts the occurrence of variables inside terms in function position: rigid text allows arbitrary terms to occur in relation position, and names in relation position may be bound by quantifiers.
This means that the content of a non-rigid text can often
be expressed in equivalent rigid text by unpacking all the non-rigid terms and
replacing them with suitable relational atoms, for example by re-writing
(forall (x y)( ... (R ((f y) x)) ... ))
(forall (x y) (exists (z) ( ... (and (R (z x)) (f z y) (functional f))) ...
)))
with the additional axiom:
(forall (f) (iff (functional f) (forall (x y)(implies (and (f x @z)(f
y @z)) (= x y)))))
If all terms are names, so there are no expressions in function position, the text is pure relational.
It is useful to distinguish a subset of the core syntax which is just sufficient to define the meanings of all the other logical constructions. The semantics will be defined on this minimal 'kernel', and the meanings of the remaining constructions defined by a systematic translation to the kernel. The kernel expression syntax is a subset of the Core syntax:
termseq ::= (term S?)* seqvar?
term ::= name | '(' S? term S termseq S? ')' | '('quotedstring S term S? ')'
atom ::= '(' S? term S termseq S? ')'
boolsent ::= '(and' S (sentence S?)* ')' | '(not' S? sent S?')'
quantsent ::= '(forall' S? '(' S? name S )* ')' S? sentence S? ')'
sentence ::= atom | boolsent | quantsent | '('quotedstring S? sent ')'
sclphrase ::= sentence | '(' quotedstring ')'
scltext ::= ( S? sclphrase S?)*
and the translations of the other core expression patterns into the kernel
are given by the following table. The first line defines the meaning of role-set
atoms, discussed in more detail above: the variable x introduced
in this line is assumed to be distinct form any other names occurring in the
expression. The remaining translations are the standard textbook reductions
of logical expressions to the forall-and-not subcase.
| expression E of type | with syntactic form | translates to kernel expression K[E] |
| atom | (t (roleset: (n1 t1) ... (nm tm))) |
K[ (exists (x) (and (t
x) (n1 t1 x) ... (nm tm
x))) ] |
| boolsent | (or s1 ... sn) |
(not (and (not K[s1])
... (not K[sn])
)) |
(implies s1 s2) |
(not (and K[s1]
(not K[s2])
)) |
|
(iff s1 s2) |
(and K[ (implies s1 s2) ]
K[ (implies s2 s1)] ) |
|
| quantsent | (forall (x ...) s) |
(forall (x) K[ (forall (...) s) ]
|
(forall ((x t) ...) s) |
(forall (x)(implies (t x) K[ (forall
(...) s) ] )) |
|
(exists (...) s) |
(not K[ (forall (...) (not K[
s ])) ] |
Consider any SCL kernel text no seqvars T written using names from some vocabulary V. One can translate this into a GOFOL text ha[T] with essentially the same meaning by applying the holds-app translation.
Might be best to do this without treating = specially, and distinguish these cases as ha= and rha=. Make his decision later when the lemmas are written.
This translation does not fully describe the embedding. One needs axioms to capture = and also to capture the relation-function convention, eg (implies (= x (R y)) (R x y)) is a tautology but translates into a nontautology in GOFOL, viz (implies (= x (app-2 R y))(holds-3 R x y)). Need to state the full translation into a theory after the purely syntactic translation.
This kind of example is also the one that involves an
entailment asymmetry arising from the signature conditions, which is the only
unconventional aspect of SCL entailment. Maybe (??) it would
be easier to not build this in, particularly as we can state it using seqvars
by writing
(forall (x R) (iff (= x (R @z)) (and (R x @z) (forall (u v)(implies (and (R
u @z)(R v @z)) (= u v))))))
so it could be included in a standard header, and the proof theory would get
a lot simpler. The only snag is that there really is no semantic justification
for distinguishing functions from functional relations!
The signature of ha[T] contains all of V, classified as individual
names, plus the countable sets {holds-0, holds-1,...}
of relation names with arities respectively 1, 2, ... and {app-0,
app-1,...} of function names with arities respectively 2, 3,...
, and the translation maps terms and atoms of T into those of ha[T]
by the recursive application of the following translation rules to every atomic
sentence in T
for any name n, ha[n] = n
for any term (t t1 ... tn), ha[(t t1 ... tn)] --> (app-n ha[t] ha[t1] ... ha[tn])
for any atom (t t1 ... tn) with t not equal to '=', ha[(t t1 ... tn)] --> (holds-n ha[t] ha[t1] ... ha[tn])
For example,
ha[(forall (x y) (implies (Boy x)) (exists (y) (and (Girl y)
(Kissed x y) (= y (lover x)) )))]
=
(forall (x y) (implies (holds-2 Boy x)) (exists (y) (and (holds-2 Girl
y) (holds-3 Kissed x y) (= y (app-2 lover x)) )))
The relation and function names of ha[T] play no real expressive role: they exist merely to provide a GOFOL 'wrapper', allowing every name in V to be treated uniformly as denoting non-relational entities in the universe, i.e. individuals in GOFOL.
Later we will show that T is satisfiable iff ha[T] is: in fact, that any model of T can be transformed into a model of ha[T], and vice versa. The construction is fairly obvious.
If some symbols of V occur only in relation position in T, then a more restricted translation can be used in which the translation rules above are applied only to terms and atoms in V whose leading term has a subterm which also occurs in an object position, so that any parts of the vocbaulary which are strictly first-order are left unchanged by the translation. We will refer to this as rha[T]. For example, rha leaves the above example unchanged. This restricted translation is idempotent on GOFOL texts, unlike the full translation; but it has the severe practical limitation of not being preserved under textual combinations.
Write T+S for the text obtained by concatenating the texts T and S, then we have for any T and S,
ha[T] =/= T
and
ha[T+S] = ha[T] + ha[S]
In contrast, for any GOFOL text T,
rha[T] = T
so that for example rha[rha[T]] = rha[T]; but there exist texts T and S with
rha[T+S] =/= rha[T] + rha[S].
This will occur whenever a name is in object position in S but only in relation position in T, for example. An application which is translating SCL into GOFOL using rha could therefore find itself needing to re-apply the translation mapping when new sentences are added to a text, which is likely to be an unacceptable cost for many applications.
Part of the intended function of the SCL header is to allow an SCL module to 'declare' explicitly which of the symbols in its vocabulary do not occur in object position, enabling an SCL engine to safely translate SCL into GOFOL using the more efficient restricted rha mapping.
For convenience later, we define the inverse syntactic mappings ah and ahr by the equations ah[ha[x]] = x and ahr[rha[x]] = x
remark that seqvars can be translated using lists, which gets the whole language into GOFOL.
The semantics of SCL is defined in terms of a satisfaction relation between SCL text and structures called interpretations, in the conventional way. For SCL however the interpretations are required to extend the relational mapping into the domain so as to provide an appropriate relational interpretation for every individual which may be denoted by a term in a relation position. As discussed earlier, this generalizes the usual idea of an interpretation being defined on a fixed signature. In effect, this restricts interpretations to be those which would fit any signature under which the text could be considered to be syntactically legal.
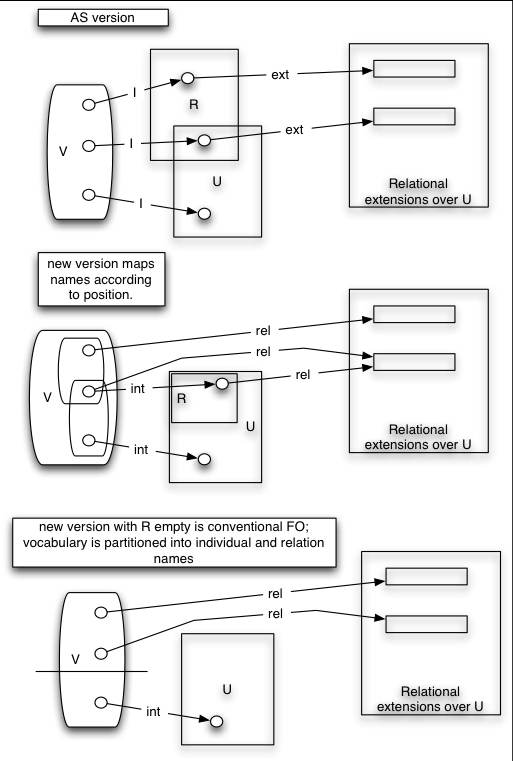
February 2004. The following has now been slightly modified. int maps to individual values, rel maps from names (in the vocabulary) to extensions. Rather than changing rel, there is now a mapping relation from names union relational individuals which is rel on pure relation names and rel+I on individuals. This makes it less awkward to state the semantics, and the 'fitting' conditions can be simply stated as conditions on relationwhcih require it to extend properly into the universe to handle all denotations of any expressions (not just names) which occur in functinal position. This makes the whole thing even more like a conventional FO interpretation: without the extension of relation into U, it is exactly a conventional FOI.
I havnt bothered to re-draw the diagram, which is not intended to be included in the final version of this document.
This is essentailly the same MT as in Chris' document, but with the ext mapping treated differently. Heres the summary picture:

The idea is to give an intuitive story for what 'ext' (now rel) means: its the extension of the ordianry semantic mapping for relation *symbols* into the universe so as to provide for individuals playing the role of relations. This is quite a pretty picture: one can view the 'fitting' conditions as a kind of induction which forces rel into the universe in appropriate ways to ensure that enough relations exist - but its chief advantage is that it preserves the GOFOL case strictly, in that the MT is then exactly conventional.
The downside is that the MT conditions for atoms and terms have to be stated twice, once using rel(v) for relation names and onceusing rel(I(t)) for other terms; but IMO this is a small price in elegance, I think. Also having a lexical category of 'pure' relation symbols even in the full wild-west syntax is quite useful eg in simplifying the holds/app translation. And it clarifies why some relations need not be in the universe.
This combines Chris' idea for handling the Horrocks sentences by allowing R to escape U with the older idea of R being the subset of U which is the relational individuals. We adopt the latter, but handle the former by letting relation names which are not used as individuals to denote extensions directly. This has no consequences for intensional relational theories since they always have those relations in the universe in any case.
Let T be an SCL text, VO(T) be the set of names occurring in object position in T and VR(T) be the set of names occurring in relation position in T, called respectively the object and relation vocabularies of T.
An interpretation of T is defined initially by a set and two mappings:
A nonempty set UI called the universe;
A mapping intI from VO(T) to UI;
A mapping relI from VR(T) to the set RelI of sets of finite sequences of elements of UI
such that if v is in function position on n in T then relI(v) is functional on n.
This is a conventional first-order interpretation structure; although in SCL the two vocabularies are not required to be disjoint.
SCL needs to extend this to account for the interpretation of expressions in which a term other than a name, or a term containing variables, occurs in a relation position. In these cases, we will assume that the individual denoted by the term plays the role of a relation. This requires that that the relI mapping is extended to any individual in the universe which can be the denotation of a term in relation position in T. We will refer to the set of such relational individuals as RI and the extended mapping as relationI. It is convenient to have relationI include relI; so, formally, an interpretation also involves another set and mapping:
A subset RI of UI ;
A mapping relationI from (RI union VR(T) ) to RelI which is identical to relI on VR(T) and which satisfies
the basic fitting condition: for any v in VR(T) with intI(v) in RI, relationI(intI(v)) = relI(x);
and the conditions described in the table below.
Note that the
Define a name map on a set S of names to be any mapping from S to UI, and a sequence map to be any mapping from sequence variables to finite sequences of elements of UI. If A is a name or sequence map on S, define IA to be the interpretation which is like A on names or sequence variables in S, but otherwise is like I: formally, UIA = UI, relationIA = relationI, and intIA(v) = A(v) when v is in S, otherwise intIA(v)= intI(v).
This notation associates to the left, so that IAB = (IA)B, meaning that if x is in the domain of B then intIAB(x)=B(x).
Note, this cheats slightly since seqvars aren't names in a vocabulary. Sigh, I guess I should make more fuss about this.
The interpretation I(E) of any SCL core expression E, and the further conditions on the relationI mapping, are then combined in the following table.
| SCL interpretation I of an expression E | |||
| if E is a | of the form | I is an interpretation of E if | and I(E) = |
| name | name, in object position |
intI(name) |
|
name, in relation position |
relationI( if I( |
||
| term sequence | (t1 ... tn) |
<I(t1),..., I(tn)> | |
(t1 ... tn @v) |
<I(t1),..., I(tn) ; I(@v)> |
||
| term | (f seq) |
If I( relationI( |
x, where relationI(f) contains
<x ; I(seq)> |
('string' term) |
relationI(('string' term))
= relationI(term) |
I(term) |
|
| atom | (r seq) |
If I(f) exists then I( f) is in RI and relationI(f)
= relationI(I(f));otherwise relationI( f) = relI(f). |
true if relationI(r) contains I(seq),
otherwise false |
| booleanSentence | (not s) |
true if I(s) = false, otherwise false |
|
(and s1 ... sn) |
true if I(s1) = ... = I(sn) = true, otherwise
false |
||
(or s1 ... sn) |
false if I(s1) = ... = I(sn) = false, otherwise
true |
||
(implies s1 s2) |
false if I(s1) = true and I(s2) = false, otherwise
true |
||
(iff s1 s2) |
true if I(s1) = I(s2), otherwise false |
||
| quantifiedSentence | (forall (var) body) |
for any name map B on {var}, IB is an interpretation
of body |
if for every name map B on {var}, IB(body) =
true, then true; otherwise, false. |
(exists (var) body) |
if for some name map B on {var}, IB(body) =
true, then true; otherwise, false. |
||
(forall ((var t) body) |
for any name map B on {var}, IB is an interpretation
of body and of (t var) |
if for every name map B on {var}such that relationI(t)
contains <B(var)>, IB(body) = true, then
true; otherwise, false. |
|
(exists ((var t) body) |
if for some name map B on {var}such that relationI(t)
contains <B(var)>, IB(body) = true, then
true; otherwise, false. |
||
| sentence | ('string' sentence) |
I(sentence) |
|
| phrase | ('string') |
true |
|
sentence |
for any sequence map A on the seqVars in sentence, IA is
an interpretation of sentence. |
if for every sequence map A on the seqVars in |
|
(scl:imports name) |
I is an interpretation of I(name) |
false if I(I(name)) = false, otherwise true |
|
| scltext | s1 ... sn |
I is an interpretation of all of s1 ... sn |
true if I( |
The conditions in the third column in effect extend the basic fitting condition from simple names to all expressions, so that if E is any expression in relation position, then relationI(E) = relationI(I(E)); and if E occurs in a function position on n then relationI(E) is functional on n; and moreover, if E contains variables bound by quantifiers then no matter how the variable is interpreted (over the universe of the interpretation), the expression denotes an entity with a suitable relational interpretation defined by relationIA.
To see the effect of these conditions, consider the atomic sentence
((mainproperty a) b c)
Here, the term (mainproperty a) is required to denote something
in the universe but it is also required to play a relational role, so I((mainproperty
a)), that is, the individual x with <x, I(a)> in relationI(mainproperty),
is in RI; and therefore relationI( (mainproperty
a)) is defined and relationI(I( (mainproperty
a) )) = relationI((mainproperty a)).
Because this applies for all variable maps, the presence of a variable in a relation position, for example
(forall (R) (iff (transitive R) (forall (x y z)(implies (and (R x y)(R
y z))(R x z))) ))
requires that the entire universe of any interpretation consist of relational individuals, so that RI = UI and relationI(x) is defined for any x in the universe.
To see why, observe that R occurs in relation
position so relI(R) is defined; now choose
some x in UI and consider the variable map A with A(R)
= x, so IA(R) = x. IA is required to be an interpretation of the
body
(iff (transitive R) (forall (x y z)(implies (and (R x y)(R y z))(R
x z))) )
(R x y)
and hence of the name R occurring in relation position; and since
IA(R) exists, x must be in RIA which, by definition,
is RI.
However, this is in fact a trivial requirement, since one can simply define relationI(x) = { } for all x to which no stronger constraint applies. The presence of a variable in a function position requires all individuals to be associated with nonempty functional extensions: this too can always be trivially satisfied, for example, by choosing a universal functional value c in the universe and defining relationI(x) to be the set of all tuples <c,...> with c in first position, for all x in T. This makes everything in the universe into a relational individual with a fully functional extension for every arity. Of course, this interpretation may not satisfy the text, but its possibility does ensure that the truth-recursions which define satisfaction are well-defined.
These requirements on the relational interpretations can be read off the atom
and term syntax. For example, if there is an atomic sentence of the form ((a
x) z) where x is a variable, then relationI
must map a, and hence I(a), into a 1-functional extension,
every value of which must be mapped by relationI into a
relation. (Note that this second requirement applies only to the range of I(a),
which may be only a small part of the universe.) The presence of a sequence
variable in the body of a term with a variable in the function position, such
as the enclosed subterm in the atomic sentence (R (x @z)), imposes
a strong requirement on relationI : it must map everything
in U to an extension which is functional on every arity. These strong
requirements only arise in non-rigid text.
The fitting conditions apply to any interpretation, not just to those which satisfy the text. They are necessary structural conditions which are required to hold of every interpretation: a structure which fails to satisfy these conditions would fail to provide denotations for some expressions or fail to assign a truth-value to some sentences. One way to think about these conditions is that they are in a sense the minimal outcome of a process of negotation concerning the appropriate signature role of a name. Suppose two agents A and B are negotiating about the denotation of a name: A wishes it to denote something in the universe of discourse, while B wishes it to denote a relation. They can both be satisfied if the entity that A takes to be the denotation is allowed to play the role of a relation when the name denoting it occurs in a relation position, and if the relational extension it uses in that role is identical to the relation denoted by the name; for then, all the relational assertions that B wishes to hold will be preserved. Thus, A and B can agree. The fitting conditions are the result of following this hypothetical negotiation through the recursions defined by the semantic truth-conditions, in order to ensure that A and B can both assign a meaningful agreed interpretation to every possible instance of every expression. Note that this hypothetical negotiation does not require that any items be added or removed from the universe, or changes to the basic interpretation mappings intI and relI: it is wholly concerned with the appropriate adjustments to the mapping relationI as applied to items in the universe of discourse.
In addition to the basic semantic conditions, interpretations are required to satisfy constraints on the interpretations of the SCL special names, summarized in the following table.
| Special name | satisfies condition |
| = | relI(=) = {<x, ..., x>: x in UI
} |
scl:Distinct |
relI(scl:Distinct) = {<x1, ..., xn>:
x1,...,xn all in UI and xi =/= xj for 1<= i,j <=n} |
numeral n |
intI(n) = the decimal value of n |
quoted string 'string' |
intI('string') = string
with '\'','\\'' and '\\' replaced by ''','"' and '\' respectively.Should
give an actual string-normalization algorithm in the text and refer to it
here |
scl:Integer |
relI(scl:Integer) = {<n>: n an
non-negative integer in UI} |
scl:String |
relI(scl:String) = {<u>: u a Unicode
character string in UI} |
scl:Thing |
relI(scl:Thing ={<x1,...,xn> :
x1,...,xn all in UI } |
scl:Rel |
relI(scl:Rel) ={<x1, ..., xn>:
x1,..., xn all in RI } |
scl:Fun |
relI(scl:Fun) ={<m, x1,
..., xn>: x1,...,xn all in RI
and relationI(x1) ,..., relationI(xn)
all functional on m } |
scl:arity |
relI(scl:arity) ={<m, x1,
..., xn >: x1,...,xn all in RI
and relationI(x1) ,..., relationI(xn)
all contain an s with length(s)=m } |
All SCL dialects and extensions are required to satisfy these general conditions. Other SCL dialects and extensions may also impose semantic conditions on other categories of special names; some examples are given later.
Say that an interpretation I satisfies an SCL text T when I is an interpretation of T and I(T)=true; and that S entails T when every interpretation which satisfies S also satisfies T; that T is unsatisfiable when it has no satisfying interpretations; and that it is valid when it is satisfied by every interpretation of it.
All of these definitions are standard, but the fact that SCL interpretations are to some extent selected by the text itself does give SCL some slightly unusual semantic properties, since a text may have interpretations which are not legal interpretations of a larger surrounding text. For example, the text
(R a b)
is satisfied by interpretations in which relI(R)
is not functional, but if we add a piece of text which uses the symbol in a
functional position:
(R a b) (= a (R b))
then the interpretations of this larger text are required to provide a 2-functional relational interpretation of the symbol. This means for example that
(implies (R a b) (= a (R b)) )
is valid, since the semantic conditions guarantee that only interpretations
I in which relI(R) is functional can satisfy
this entire text, but that
(R a b)
alone, as an isolated piece of SCL text, does not entail
(= a (R b))
Simply using a name in a functional position in effect makes an implicit assertion that the entity it names has a functional extension. In a more conventional syntax, such a claim would be built into the signature and hence be satisfied automatically.
As this example illustrates, the deduction theorem is not strictly true for
SCL text: there can be S and T with (implies S T)
valid, but S not entailing T. However, this can happen only when a symbol occurs
in a functional position in T but not in S: in effect, when S and T can be considered
to be expressions in languages which have different signatures.
This point can be used to motivate headers as a device for fixing signatures when required.
Might be nice to review some standard stuff, eg prove Herbrand theorem (?) and establish some basic inference rules. One way to do this
The central issue here seems now to be whether to make the XML 'readable' or to go with the XSD-based form produced by the
An SCL module is a named piece of SCL text, called the body text,
with an optional formal preamble called a header. A module without
a header is simply a named piece of SCL text which can be imported into other
text by using the name inside an scl:imports expression, similar
to an OWL ontology [refOWL].
Headers provide another level of functionality. The header is itself SCL text, interpreted using the same semantics (and hence subject to the same inference processes) as other SCL text; but the relationship between the semantics of the header and body text is special: in particular, the header is allowed to quantify over entities which are not in the intended universe of discourse of the body text. The primary intended roles of a header are to allow a module to describe its signature explicitly, to state syntactic conventions used in the body of the module, and to delineate and provide a name for the intended universe of discourse. These are often thought of as syntactic issues requiring translations between distinct languages: following the design principles of SCL, they are here handled withing the same language by using the same uniform semantic framework, allowing SCL processors to reason about the content of SCL modules. By convention, however, any inconsistency between the header of a module and the body text may be considered to be a syntactic error in the body text.
Headers may be defined to be countably infinite, provided that the effect of such an infinite header can be reproduced by a suitable computable operation on expressions. This convention can be used to provide a semantic connection between procedural 'attachments' or 'call-outs' and the model theoretic semantics, and to provide a coherent approach to the incorporation of data-structure conventions into SCL. This conventions, together with the use of the module naming convention, allows headers to describe certain kinds of 'closed-worlds', for example allowing SCL modules to act like databases when required.
-------------------
There are 2 issues here. ONe is simply the advantages of being able to check syntax and provide guarantees of mergability and of being in a particular subcase. The other is this whole business of comparing universes of discourse and merging requiring protective guards on quantifiers.
In order to describe the interpretation of headers we need a new semantic notion. Say that an interpretation I is a shrinking of J, and that J is an expansion of I, when I can be obtained from J by deleting some things from the universe of I and possibly some names from the vocabulary. Formally, when the vocabulary of I is a subset of that of J, intI(v) =intJ(v) and relJ(v)=relJ(v) for all v in the vocabulary of I; UI is a subset of UJ, RI is a subset of RJ, and for all x in RI, relJ(x) = relI(x). Intuitively, the expansion J may include new individuals and some entirely new relations, but it cannot change the extensions of relations named in I.
Then the semantics of a module with a header can be stated as follows: an interpretation I fits a module when it is an interpretation of the body and has an expansion which satisfies the header, and it satisfies the module when it fits the module and satisfies the body:
| if E is a | of the form | then I(E) = |
| module | (scl:head head ) body |
if I(body)=true and for some
expansion J of I, J(head)=true,
then true; otherwise false |
Note that an interpretation which satisfies the body but which cannot be expanded
to satisfy the header is considered to be a non-fitting interpretation of the
module: this is the sense in which the conditions expressed by the header are
considered syntactic.The four relation names scl:Ind, scl:Rel,
scl:Fun and scl:Arity are called the header vocabulary.
The header vocabulary can be used anywhere in any SCL text; but when used in a module header, the semantic conditions require that the header classifications are understood to refer to interpretations of the body of the module, rather than of the header itself. To see the difference this makes, consider the following module with an empty header:
(scl:module example1 ( (not (scl:Ind R)) ))
This is a contradiction - has no satisfying interpretations - since any interpretation
which fits the inner sentence would require R to denote an individual
in U, but the sentence asserts that is not in U.
The sentence
(forall (x) (scl:Ind x))
is a tautology in any module body, since scl:Ind is true of everything
in the universe: one could in fact transcribe (scl:Ind term)
in the body (though not in the header) as any tautologous assertion, in particular
as ( term = term ).
However, the same sentence in the header yields a satisfiable module:
(scl:module example2 ((scl:head (not (scl:Ind R)) ) (R a) ))
This is satisfied for example by an Herbrand interpretation
H in which the interpretation mapping is the identity, with UH={a},
RH={R} and extH(R)={<a>};
the fit is guaranteed by the extension J with UJ={a,
R}, RJ={R, scl:Ind} and extJ(scl:Ind)={<R>}.
Note that although R is an individual in J, it is not in H; and
that the interpretation rules for the entire module require that extH(scl:Ind)
= {<a>}.
If the body of the module had 'mis-used' the relation symbol as an individual name, for example:
((scl:head (not (scl:Ind R)) ) (Q R) )
then once again the module would be unsatisfiable, since there are no interpretations which fit such a module, so no interpretations which satisfy it. It is useful to distinguish this kind of unsatisfiability from an unsatisfiability arising from a simple contradiction in the body of the module, such as:
( (Q R) (not (Q R)) )
since in the former case the body alone is satisfiable. The contradiction in the first case arises from an essentially syntactic incompatibility between the fitting conditions proscribed by the header and the actual usage in the body.
We will describe this case, of a module which has no interpretations which fit it, as an unfit module. Unfit ontologies have no interpretations, so have no satisfying interpretations; but their unsatisfiability arises from a different source than a mere contradiction. SCL applications may consider an unfit module to be a syntactic error, even if the unfitness can only be detected by semantic reasoning processes.
The header vocabulary can be used in fairly obvious ways to 'declare' constraints
on the allowable signature of a module. A conventional first-order language
can be specified by asserting scl:Ind of every individual, scl:Rel
of every relation, and scl:Fun of every function, and specifying
the arity of each relation and function using scl:Arity. For example,
the following header specifies a small conventional first-order language signature
suitable for expressing the earlier example:
Need a different example
Im not entirely happy with this header vocabulary. It would be better to have the ontology name itself be used as the name of its universe. This would allow one module to refer to the universe of discourse of another universe, and allow 'bridging' ontlogies to declare relationships between alternative universes of discourse. The arity/relation/function stuff is really only needed for syntax checking, but the universe of discourse is something deeper.
Which leads to the following thought. We need to be able
to say that something is(/is not) in the universe of discourse, preferably in
a way which can also be used meaningfully in another ontology. Which suggests
a 'universe' functional, eg (scl:UOD ontologyname). The problem with this might
be that it uses non-GOFOL notation essentially: ((scl:UOD foo) x). Or we could
have a general convention that an ontology name used as a predicate is that
ontology's 'thing' classification... but this overloads the ontology name, which
the W3Cers won't like. OK, need to take a decision on this.
It smells like the datatype trick of using the name both as a class and as a
function. That overloading works OK, though, so why not this one?
BUt to return to the general point: what else do we need in the header vocabulary? To allow 'type checking' we need to be able to declare arity and functionality. Do we really need an explicit Rel?? Ans: yes, becus it has a direct syntactic check associated with it.
If Ind is relativized to an ontology, why aren't Rel and
Fun also relativized? Ans: because Ind alone is connected with the quantifiers
and with equality. In fact we need to get this connection with = sorted out
better. Maybe = is enough: (ind x) is just (= x x). Aha! We havnt said
what happens to the special vocabulary conditions in an expansion:
clearly this is of critical importance, need to get it right. This might be
the key.
Surely we will want = to mean = even in the header, right? So that meaning must
be extendable, which already is a problem with the definition of expansion given.
NEEDS MORE THOUGHT.
All of this is tightly connected with the SCL->GOFOL embedding and the need to treat = specially. There is one important thing hidden here which I havnt got it completely straight yet. The idea is that when talking about A from 'outside', one has to interpret its quantifiers as restricted to its universe. The header has to be explicit about this 'outside' view.
Another thought: should importing be sensitive to the UOD? That is, the simple OWL-inspired importing is based on this unrealistic notion of a shared UOD, maybe we need to do better since we are facing up to this issue. But the simple case must be available as a syntactic default, so how do we manage that? One guideline is that importing a plain module ought to be the default case: which suggests that it is the header itself which declares the universe of discourse; just plain SCL text has no such committment. In turn suggests analysing more carefully what that process of naming really amounts to. Importing M requires that (OUD M) is the universe of the quantifiers in the sentences of M. Importing text is just a committment to satisfy it. On this view, then, giving a name to a module is a bigger deal; but what has that got to do with the header?? Nothing, so we don't get the easy default. Hmmm.
The older intuition was that one could transfer the header into the body with some quantifier restrictions. If so, importing these ought to be similar.
(scl:head
(forall (x) (not (and (scl:Ind x) (scl:Rel x) )))
(scl:Rel Boy Girl Kissed)
(= 1 (scl:Arity Boy))
(= 1 (scl:Arity Girl))
(= 2 (scl:Arity Kissed))
)
The first sentence expresses the conventional that relation symbols must not be used as individual names and vice versa: this is satisfied by every conventional first-order signature. The arity assertions here take advantage of the SCL fitting conditions. Note that it is consistent to allow a relation to take several different numbers of arguments, in general, so for example this is consistent:
(scl:Arity 2 R) (scl:Arity 3 R) (scl:Arity 5 R)
but the use of 'scl:Arity' in a function position requires
that it denote a functional relation in any fitting interpretation; so the only
consistent way to interpret this header is with scl:Arity interpreted
as a functional relation, ensuring that all relations in the body have a fixed
number of arguments.
Note that if the body of a module is syntactically correct GOFOL, then including the appropriate header does not impose any extra conditions on the fit of an interpretation. It does however make these conditions explicit so that they can be checked.
Headers may also be used to declare special names of various forms. By convention, a header may be specified to be (equivalent to) a special name theory which consists of an recursively enumerable set of ground axioms specifying the positive and negative cases of some lexical categorization, typically the lexical space of a datatype represented by a predicate. Such headers can be imported into other headers, serving there as a form of declaration that the lexical forms are considered to be special names in the module body. In particular, SCL recognizes the built-in datatypes in XML Schema Part 2: Datatypes [XML-SCHEMA2], listed in the following table:
For each such name xsd:sss, the corresponding special name header
consists of the axioms
(xsd:sss (xsd:sss name))
for each name which is a legal lexical
form for xsd:sss;
(not (xsd:sss (xsd:sss name)))
for each name which is not a legal
lexical form for xsd:sss;
(= (xsd:sss name1) (xsd:sss name2))
for each pair of names which are legal lexical forms for xsd:sss and
map to the same item in the value space of xsd:sss. The datatype
name serves here both as a function (mapping the lexical form to the value)
and as a predicate on the value space: this follows the convention used in RDF
[refRDF]. In addition, we use the datatype URI reference as the name for the
module, so that the appropriate datatype can be included in a header by writing
for example:
(scl:import xsd:nonPositiveInteger)
in the header. Note that importing a special name theory into the body of a module amounts to including an infinite set of axioms, but importing it into a header only imposes the appropriate semantic conditions on the special names actually used in the the vocabulary of the body.
When the header of a module imports a special name theory, then all the legal lexical forms of the theory are considered to be special names in that module.
The two remaining constructions allow ontologies to be given global names and to be imported into other ontologies. The idea of naming a module makes sense only if we can assume some 'global' naming convention which has a larger scope than a single module, and which interpretations are required to respect. In XCL we will use URI references as global names. in accordance with the emerging WWWeb conventions, which are elaborately described elsewhere. For semantic purposes, we simply assume that there is a fixed function ont from module names to module values. The exact nature of module values is not specified, other than that they are entities which can be parsed into SCL kernel syntax and to which an interpretation mapping can be applied. (One can think of a module value as a quoted string containing a character representation of a module written using the kernel syntax.)
| if E is an | of the form | then I(E) = |
| topsentence | (scl:import name) |
false if I(ont(name)) = false, otherwise true |
| module definition | (scl:module name = (text)) |
if for any interpretation J, J(ont(name))
= true iff J(text) = true, then true; otherwise false. |
An assertion of a module definition is required to have miraculous semantic powers: if it is ever true in any interpretation, then the name is attached to the defined module in all interpretations. Thus, if by convention we say that publishing any SCL module definitions amounts to asserting it, then a publication of a module definition requires any interpretation of any SCL module containing an importation of that name to treat it as having the same effect as copying out the sentences of the defined module in place of the importation. To actually achieve such miraculous powers requires a global naming convention: XCL uses universal resource identifiers [refRFC2396] for this purpose.