Latest version of this document: http://www.ihmc.us/users/phayes/IKL/SPEC/SPEC.html
IKL is an extension of ISO Common Logic [CL], extended with the ability to talk about the propositions that its own sentences express, and to describe its own referring names as character strings. The syntax of IKL is similar to that of the CLIF dialect of CL, but differs in some respects (it allows numerals and character strings to be used as opertors, omits the guarded-quantifer syntax and introduces numerical quantifiers.) The chief new constructions are proposition names of the form (that <sentence>), which denote propositions, and captured names of the form ('<string>'). Propositions are identified with zero-ary relations, so to apply a proposition to nothing asserts it: thus if p is a proposition then (p) is a sentence which asserts the proposition. IKL also treats quoted identifiers as zero-ary functions and requires them to evaluate to the denotation of the identifier, so that sentences of the form (= ('xxx') xxx) always evaluate to true. Together, these conventions allow for the compact expression of a variety of relationships between things, propositions, names and sentences, all within a single first-order, referentially transparent logic.
For background information about the overall design philosophy of IKL, an introduction to using IKL as a representation language and translating from other ontological formalisms into IKL, see the IKL Guide [Guide].
| syntax category | description | general syntactic form | examples |
| name | Primitive referring expression, used for all naming purposes regardless of the logical type of the thing named. |
A Unicode character string. If the string contains reserved or lexical-break characters (parentheses, whitespace, backslash, quotes) or would otherwise be considered a reserved word (numerals, sequence names) it should be enclosed inside double quotes. Backslash is used as a character escape for the double quote and for itself, and to include unicode code points for non-ascii characters in ascii text. |
|
| sequence name | Stands for an arbitrary finite sequence of things. Not supported by all IKL engines. | A Unicode character string starting with the characters '...' and which contains no other reserved characters. |
...
|
| numeral | Decimal numeral | A string of decimal digits. Leading zeros are permitted, but no decimal point, fractions, negatives or mathematical symbols. | 37
|
| quoted string | Denotes a string of unicode characters | A Unicode character string enclosed by single quotes. Backslash is used as a character escape for the single quote and for itself, and to include unicode code points for non-ascii characters in ascii text. | 'Arthur Andersen'
|
| proposition name | Denotes the proposition expressed by an IKL sentence. | The sentence itself, prefixed with the reserved word 'that'. |
(that (Taller Bill Joe))
|
| function term | Denotes the value of a function applied to some arguments | A term denoting a function, followed by an argument sequence of terms. | (f a (g b) ...) |
|
atomic sentence |
means that a relation holds between arguments | A term denoting a relation, followed by an argument sequence of terms. |
|
| equation | means that two expressions denote the same thing | An equality sign followed by two terms. | (= a b) |
| conjunction | means that all its components are true | The reserved word and followed by a sequence (set) of sentences. | (and p q r ...) |
| disjunction | means one of its components is true | The reserved word or followed by a sequence (set) of sentences | (or p q r ...) |
| implication | means that the antecedent materially implies the consequent | The reserved word if followed by an antecedent sentence and a consequent sentence. | (if p q) |
| biconditional | means that each of two sentences materially implies the other | The reserved word iff followed by two sentences. | (iff p q) |
| negation | means that its inner sentence is false | The reserved word not followed by a sentence. | (not p) |
| existential quantifier | means that its body is true for some value of the bound names | The reserved word exists, a sequence of bindings, and a body which is a sentence. | (exists (a (b c)...) p) |
| universal quantifier | means that its body is true for any interpretation of the bound names | The reserved word forall, a sequence of bindings, and a body which is a sentence. | (forall (a (b c)...) p) |
| binding | general form for indicating variables bound by quantifiers | A name; or a name together with a restriction which is a term; or a sequence marker. |
a
|
| IKL text | a collection of IKL phrases; an IKL ontology | Either a sequence of phrases, or the reserved word text, a name called the identifier, and a sequence of phrases. The identifier, if present, must be unique to the text, and provide for network support for tranmission of content, eg. an http: URI. | p q r ...
|
| phrase | top-level item in a text. | Either a sentence, a module, an importation or a commented text. | |
| module | Names a piece of IKL text and also provides a name for the local universe of discourse. The text is interpreted as talking about a 'local' universe from which some entities may be excluded. | A name, an optional exclusion list of names, and an IKL text. All quantifiers in the text are understood to be restricted using the module name, and the excluded names are required to not be in the module class. | (module View17 (excluded p q ...) r s ...) |
| importation | used to include a remote IKL text into another IKL text. | A name (which must be the identifier of an IKL text) preceded by the word imports. |
(imports ex:ListOntology) |
| commented expression | A character string which is attached to any IKL expression, without changing its meaning | The reserved word comment, a quoted string, and the expression. | (comment 'This is nonsense' |
This grammar is divided into two parts. The Lexicon part takes a character stream as input and divides it into lexical tokens (in the sense used in ISO/IEC 2382-15), each classified into one of seven disjoint syntactic types, while handling whitespace issues. The subsequent parts of the grammar assume an input consisting of a stream of lexical tokens rather than a stream of characters.
Char = <any Unicode character> ;
NameChar = Char - ( <white space character> | '(' | ')' | ''' | '"' ) ;
NameItem = NameChar, { NameChar } ;
EnclosedNameEscape = '\"' | '\\' ;
EnclosedName = '"', {(Char - ('"' | '\')) | EnclosedNameEscape}, '"' ;
SeqName = '.', '.', '.', {NameChar} ;
Digit = '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9' ;
Numeral = Digit, {Digit } ;
CharStringEscape = '\'' | '\\' ;
CharString = ''', {(Char - (''' | '\')) | CharStringEscape}, ''' ;
SimpleName = NameItem - (EnclosedName | Numeral | CharString | SeqName) ;
Open = '(' ;
Close = ')' ;
LexicalToken = Open | Close | EnclosedName | SeqName | Numeral | CharString | SimpleName ;
The job of the lexical analyzer is to break a character stream into a stream of lexical tokens while discarding any intervening whitespace. Any character string which cannot be so divided is a lexical error. Lexical errors may arise from the mis-use of the escaping character inside quoted strings or enclosed names, as in 'ab\c', or by the input terminating without balancing quotes, as in 'a b /' xy .
The rest of the grammar assumes that lexical analysis is completed, and so takes as input a stream of lexical tokens.
For convenience below, we define the corresponding character sequence of an EnclosedName (resp. CharString) to be the sequence of Unicode characters gotten by erasing the outer double (resp. single) quotes and the first backslash character in every EnclosedNameEscape (resp. CharStringEscape). The corresponding character sequence of a SimpleName or a Numeral is simply the sequence of characters in the name or numeral itself.
IKLName = 'that' | 'comment' | '=' | 'not' | 'and' |'or' | 'if' | 'iff' | 'forall' | 'exists' | 'text' | 'module' | 'import' | 'excluded' ;
Name = (SimpleName | EnclosedName) - IKLName ;
PropName = Open, 'that', Sentence, Close ;
FixedRefName = Numeral | CharString | PropName ;
BindingName = Name | SeqName ;
ThingName = Name | FixedRefName ;
Comment = CharString | EnclosedName ;
Term = ThingName | Open, Term, ArgSeq, Close | Open, 'comment', Comment, Term, Close ;
ArgSeq = { Term | SeqName } ;
Atom = Open, Term, ArgSeq, Close | Open, '=', Term, Term, Close ;
Boolean = Open, 'not', Sentence, Close | Open, 'and', { Sentence }, Close | Open, 'or', { Sentence }, Close | Open, 'if', Sentence, Sentence, Close | Open, 'iff', Sentence, Sentence, Close ;
Quantified = Open, 'forall', [Numeral|Name], Open, {Binder}, Close, Sentence, Close | Open, 'exists', [Numeral|Name], Open, {Binder}, Close, Sentence, Close ;
Binder = BindingName | Open, BindingName, Term, Close ;
Sentence = Atom | Boolean | Quantified | Open, 'comment', Comment, Sentence, Close ;
Text = {Phrase} | Open, 'text', Identifier, {Phrase}, Close ;
Module = Open, 'module', Identifier, [Open, excluded, Name, {Name}, Close], {Phrase}, Close ;
Phrase = Sentence | Open, 'comment', Comment, Text, Close | Open, 'import', Identifier, { Identifier }, Close ;
Identifier = Name ;
The intention here is that identifiers are a special class of names which can also be used to locate IKL text on a network. For example, IRIs serve this purpose for the Web. Thus, an identifier is both a logical name within IKL, and also a network identifier. To maintain internal coherence, these two uses should be coordinated, in that the IKL denotation of an identifier is understood to be a proposition expressed by the identified text or module, according to the IKL semantic recursions. This whole subject is discussed more fully in [CL].
The IKL semantics follows the Common Logic semantics closely but with two new extensions, both of which use the special case of a relation or function with no arguments. Relations with no arguments are identified with propositions, and character sequences corresponding to names, when used as functions with no arguments, are required to evaluate to the denotation of the name. In this way, a zero-ary use of a name in an atom corresponds to the assertion of a denoted proposition, providing the same expressive power as a truth predicate, while the zero-ary use of a quoted name in a term amounts to a form of de-quotation. These are described semantically by imposing extra conditions on interpretations.
A vocabulary V is the union of disjoint sets VN of names and VS of sequence names. V and the grammar of IKL together determine a set VP of proposition names. An IKL interpretation structure I of V is a single 'possible world' consisting of a set UI called the universe, and two mappings relI from UI to 2|UI*, the set of subsets of finite sequences of UI, and funI from UI to (UI* -> UI), the set of all functions from a sequence of elements of UI to UI and which satisfies all the additional conditions described below. An IKL interpretation of V (over the interpretation structure I) is a mapping from (VN union VP) to UI and VS to UI*; we will write this mapping as I also, and omit subscripts when no confusion would arise. If n is a name in VN and q is its corresponding character sequence, then we will say that q captures n. Character sequences which capture names in a vocabulary have a special semantic condition imposed on them in any interpretation of that vocabulary.
If I is an interpretation and N a mapping from a subset of V to U, then [I+N] is the IKL interpretation over the same interpretation structure, but with
[I+N](x) =( N(x) if x is in the domain of N, otherwise I(x) )
Sequences play a central role in IKL semantics. We write < > to denote the empty sequence. If x and y are two sequences, then x+y is the sequence obtained by concatenating them in order, i.e. if
x= <x1,...,xn> and y=<y1,...,ym>
then
x+y= <x1,...,xn,y1,...,ym>.
| if E is | then I(E) is |
| a Name or a PropName x |
I(x), an element of U |
| a SeqName ...x | I(x), a finite sequence of elements of U |
| a Numeral x | the number denoted by x considered as a decimal numeral. |
| a CharString s | the corresponding character sequence of s |
| The empty ArgSeq < > | the empty sequence < > |
| An ArgSeq <T1, ... ,Tn> where T1 is a term | the sequence <I(T1)> + I(<T2, ...,Tn>) |
| An ArgSeq <T1, ... ,Tn> where T1 is a SeqName | the sequence I(T1) + I(<T2, ...,Tn>) |
A term (T S) where S is an ArgSeq |
funI(I(T))(I(S)) |
A term (comment ST T) |
I(T) |
An atom (T S) where S in an ArgSeq |
true if I(S) is in relI(I(T)), otherwise false. |
A boolean sentence (not S) |
true if I(S) = false, otherwise false |
A boolean sentence (and S1 ... Sn) |
false if I(Si) = false for 1<=i<=n, otherwise true |
A boolean sentence (or S1 ... Sn) |
true if I(Si) = true for 1<=i<=n, otherwise false |
A boolean sentence (if S1 S2) |
false if I(S1) = true and I(S2) = false, otherwise true. |
A boolean sentence (iff S1 S2) |
true if I(S1) = I(S2), otherwise false. |
A quantified sentence (forall (x) S) |
true if for any name map N from {x} to U, [I + N]( S ) = true; otherwise false. |
A quantified sentence (exists (x) S) |
true if for some name map N from {x} to U, [I + N]( S ) = true; otherwise false. |
A sentence (comment ST S) |
I(S) |
A phrase (comment ST T) |
I(T) |
A phrase (import T) |
true if I(I(T)) = true, otherwise false. |
| A text P1, ... Pn | false if I(Pi) = false for 1<=i<=n, otherwise true |
Note that an empty conjunction is always true, an empty disjunction always false; and that a text is treated exactly like the conjunction of all the sentences in it.
This omits some IKL constructions which can be regarded as syntactic sugar, and translated into constructions which are in the above table, as follows:
| an IKL expression E of the form | means the same as its translation t[ E ] |
A quantified sentence (q ( ) S) with an empty binder |
S |
A quantified sentence (forall(x ...) S) |
|
A quantified sentence (exists(x ...) S) |
(exists (x)t[ (exists(...)S))] |
A quantified sentence (forall((x t) ...) S) |
(forall (x)(if (t x)t[ (forall(...) S))] |
A quantified sentence (exists((x t) ...) S) |
(exists (x)(and(t x)t[ (exists(...) S))] |
A numerical quantified sentence (exists n (x) S) |
t[(exists (x1 ... xn)(and (allDiff x1 ... xn)t[ S[x/x1] ] ... t[ S[x/xn] ]))] |
A numerical quantified sentence (forall n (x) S) |
t[(forall (x1 ... xn)(if (allDiff x1 ... xn)(and t[ S[x/x1] ] ... t[ S[x/xn] ])))] |
A module (module M (exclude N1 ... Nn) T) |
the text:
where T' is T, but with every binder x replaced with |
The translation given here for the module construction assumes that AND satisfies
(forall (p q x)(iff ((AND p q) x) (and (p x)(q x))))
In addition, an interpretation must fulfil certain extra reference conditions on some names, as follows:
| If E is | and I(E) is | then I must satisfy |
| A CharString s which captures a name n in V | the corresponding character sequence c of s | funI(c) contains << >, I(n)> |
a PropName (that S) |
an element x of U | relI(x) contains < > iff I(S) = true |
These are easy to satisfy provided that the universe U contains 'enough' individuals to provide suitable referents. Clearly it must contain an integer corresponding to every numeral used in any set of sentences, and enough character sequences to provide referents for every quoted string. In addition, however, the condition on proposition names means that there must be enough individuals to support the full range of propositional meanings expressed by IKL sentences. We therefore need to show that this is always possible, by giving an explicit construction. This can be done in various ways; we sketch one here for completeness, but this particular construction is not suggested as definitive. This construction treats propositions as interpreted abstract syntactic structures.
We first describe a category of syntactic structures called forms corresponding to the abstract syntactic structure of IKL sentences; more generally, of IKL expressions. Intuitively, a form is the parse tree of an IKL expression, considered as an oriented graph, in which bound names have been replaced by links back to their binding quantifier. The tips of such a graph correspond to the names which occur free in the expression, and expressions which differ only in their bound names correspond to the same form. We will refer to the form of an IKL expression, meaning the form obtained by parsing the expression. For example:
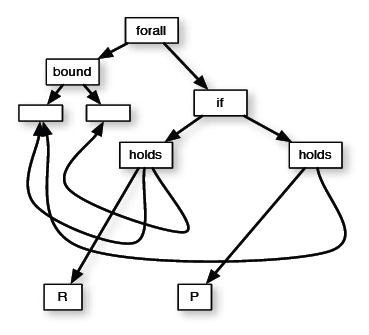
(forall (x y)(if (R x y)(P x)))

(forall (x)(if (and (P x)(sortP P)) (exists (y R)(and (TransferRelation P R)(R x y))) ))
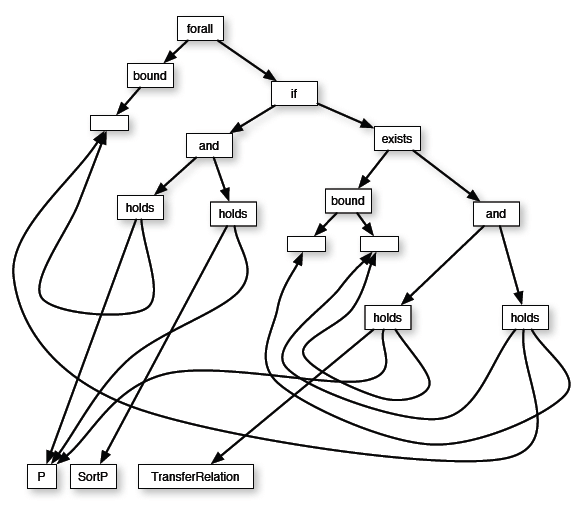
It is possible to construct such graphs which do not correspond to any IKL expression, but these are not considered to be IKL forms. Clearly, expressions which differ only in bound variable names map to the same form.
The tedious formal details of this construction are omitted here, but we note that the IKL grammar could be defined in terms of construction operations on forms, and the IKL model theory defined over forms; they amount to an alternative 'graph-based' syntax for IKL. (With a bit of extra work, they could be the basis for a scheme for encoding IKL syntax into RDF graphs, though this encoding might not respect the RDF semantics.) Note that tips with identical labels are merged, so that the number of tips of a form is exactly the number of distinct free names in an expression with that form.
A sentential form F with vocabulary N, and a mapping from N into UI, together define a proposition which is about the set {M(x): x in N} of individuals referred to by names in the form, and its truth-value is the value gotten by interpreting F in I, following the IKL truth-recursion on the form, i.e. by interpreting the form as a sentence. We will therefore define propositions to be structures similar to sentential forms, but with individuals at the tips rather than names. As with forms, we require that tips are unique.
So for example, if I('P') = I('R') = A, say, where A is an individual in the universe UI, then the proposition corresponding to the first sentential form above is this proposition:
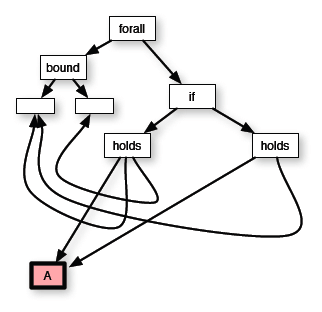
where we have used color to emphasise the semantic nature of the object at the tip. This is the proposition that if the relation A holds between two things, then it also holds of the first. This proposition is about A, by whatever name it is referred to: unlike the similar sentential form, it no longer has any free names in it.
Given a set S of individuals, the proposition extension P(S) is the set of all propositions about a finite subset of S. The universe UI is then required to contain all propositions defined over itself, i.e. to be a fixedpoint of the equation x= P(x) under the starting condition that x contain all referents of simple names, numerals and quoted strings in the vocabulary. This fixedpoint is well-defined and countable if the initial universe is, since every proposition can be regarded as composed (perhaps in many ways) from a sentential form F and a name mapping N from its vocabulary to the universe. Since sentential forms are finite, they have only finitely many constituents; hence, propositions only have finitely many. Thus for each proposition there is a finite set of things it is about, and a finite size for its corresponding sentential form, and so the propositional extension of a countable set is countable.
Here we list some logical truths which involve the new extensions to the IKL syntax.
For any name nnn,
|== (= nnn ('nnn'))
For any sentence sent,
|== (iff sent ((that sent )))
This means that the syntactic patterns ((that ...)) and (' ... ') are 'invisible'; the outer zero-ary application in effect 'cancels' the construction of the proposition name from the enclosed sentence, and that of the quoted name from the identifier. A weak version of the inverse relationship is also true:
(forall (p)(iff (p)((that (p))) ))
Note, the stronger statement (= p (that (p))) is not a tautology, since two distinct propositions might have the same extensional truth-conditions. This is a special case of the fact that in Common Logic, two distinct relations might have the same relational extension, since IKL propositions are identified with zero-ary relations. The strongest possible extensional identification:
(and
(forall (...)(iff (f ...)(g ...)))
(forall (...)(= (f ...)(g ...)))
)
is still not enough to entail the simple identity
(= f g)
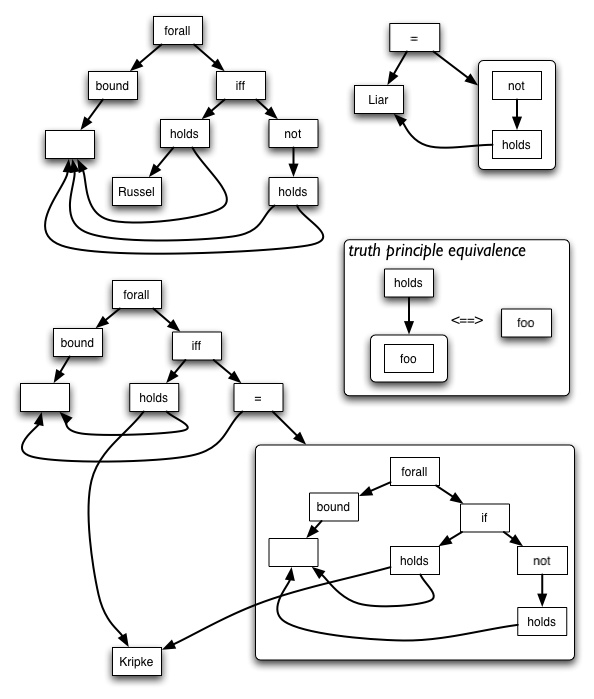
|== (not (= p (that (not (p)))))
This illustrates the fact that IKL can reproduce assertion patterns which are traditionally described as paradoxical. (= p (that (not (p)))) is a compact IKL version of the 'liar paradox', a proposition which asserts its own falsity. There is no such proposition, so this equality statement is self-contradictory, i.e. always false: so its negation, shown above, is always true. The figure shows this and some other well-known 'paradoxes' rendered as IKL forms.
July 20 2006
Incorrect introductory statement that IKL syntax is extension of CLIF syntax deleted, and brief summary of differences included. (Correcting error noted by Joshua Taylor, tayloj@rpi.edu). Minor typos corrected.
July 5 2006
1. Grammar of phrases changed to reflect recent CL edits: comments can now span several sentences in a text.
2. Model theory for and , or and texts re-phrased to make the no-argument cases work correctly.
Bill Andersen
Richard Fikes
Patrick Hayes
Charles Klein
Deborah McGuiness
Christopher Menzel
John Sowa
Christopher Welty
Wlodek Zadrozny
[CL] Common Logic - A framework for a family of Logic-Based Languages, ed. Harry Delugach. ISO/IEC JTC 1/SC 32N1377, International Standards Organization Final Committee Draft, 2005-12-13 http://cl.tamu.edu/docs/cl/32N1377T-FCD24707.pdf
[Guide] Patrick J. Hayes, IKL guide. Unpublished memorandum, 2006. http://www.ihmc.us/users/phayes/IKL/GUIDE/GUIDE.html